Model transformations are a key element in most model-driven engineering approach. But writing them is a time-consuming and error-prone activity that requires specific knowledge of the transformation language semantics.
Usually, a model-driven project involves several consecutive transformations. Intermediate steps are often implemented as model-to-model transformations, each one taking as input the output of the previous step as part of a continuous refinement process from high-level models to platform-specific ones. One last step consists in a model-to-text transformation that takes this low-level models and generates a textual output, i.e. the final code, as a result.
Domain-specific languages and tools, such as ATL, Acceleo, and Xtext, aim to accelerate the writing of model transformations by offering facilities to handle model querying, model serialization, etc.
We propose to take advantage of the advances in Artificial Intelligence and, especially in supervised machine learning, to automatically infer heterogeneous model transformations from sets of input-output examples. We use a neural network architecture composed by an encoder-decoder with an attention mechanism, where both the encoder and decoder are LSTM (Long Short-Term Memory) neural networks. Once the transformation mappings have been learned, the system is able to autonomously transform new input into their corresponding output without the need of writing any transformation-specific code. Not only are the inferred transformations able to automatically produce expected output artifacts, but they are able to oblige developers to comply to company or project standards, key to the solution’s adoption and valuable to ensure quality. We evaluate the correctness and performance of our approach and discuss its advantages and limitations.
A new ideas paper exploring this in the context of model-to-model transformations was accepted at Models’19 (download the paper here , check the presentation slides below, or keep reading for the full details), and an extended version covering heterogeneous transformations has been recently accepted at SoSyM (download a preprint of the paper). Keep reading for a summary of this line of work.
Contents
1 Introduction
AI is evolving fast thanks to the advances in hardware and the arrival of the big data era. A recent survey [1] predicts that “AI will outperform humans in many activities in the next ten years, such as translating languages, writing high-school essays, or working as a surgeon”.
AI is also starting to impact the software development processes itself. In fact, as of today, there are initiatives claiming the (prospective) applications of AI in the different phases of the software development lifecycle [2], from the requirement analysis and design to the development, testing, deployment, maintenance, etc. The main goal is always the same: help software engineers develop software easier, faster and less error- prone while being able to manage more complex problems. In this sense, the concepts of intelligent software and cognified software engineering [3], [4] have been introduced.
However, few approaches target model-driven engineering (MDE). Some exceptions are [5], to generate UML class diagrams from natural language specifications, [6] to collaboratively build domain models using chatbots, and [7] to provide a tool for classifying web images as UML static diagrams. Still, we are not aware of the existence of any solution addressing a key element of any MDE approach: model transformations.
Indeed, writing model transformations is an important but also time-consuming and error-prone process. And while there is a myriad of proposals to facilitate the definition of model transformations, we lack a solution that empowers non-expert users to autonomously transform new input models into their corresponding output models without the need of writing any transformation-specific code.
This paper proposes such a solution based on Machine Learning (ML). ML, and in particular, its supervised learning methods, enables machines to learn patterns from existing data source and make predictions about new data. Given a set of input-output data, an ML algorithms would be able to learn the mappings between the sample inputs and the outputs and, then, predict for new input data, what the output would be. The simplest example in this context is language translation. The first attempt to translate text from one language to another was to translate word by word. Afterwards, companies hired linguists to create language-specific rules and started using Statistical Machine Translation (SMT). Currently, big companies such as Google generate translations by means of Artificial Neural Networks (ANNs) [8]. We adopt a similar approach for the model transformation challenge.
In this sense, we suggest a change of paradigm in the way we approach model transformation problems and propose to rely on a ML-based framework using a particular type of ANNs, Long Short-Term Memory (LSTM) ANNs to derive transformations from sets of input/output models given as input data for the training phase.
2 Background in Artificial Neural Networks
An ANN can be seen as an structure composed by neurons with directed connections between them. Each neuron is a mathematical function that receives a set of values through its input connections and computes an output value that is taken by another connection and transferred to another neuron. Two specific types of neurons are the input and output neurons which do not have input predecessors or successors respectively and serve only as input and output interfaces to the ANN. Connections have associated weights (i.e., real numbers) that the neurons use and that are adjusted during the learning process with the purpose to increase or decrease the strength of the connection. Thus, from an analytical point of view, ANNs are complex mathematical functions composed by other functions.
Most ANNs are part of a supervised learning procedure where a tagged set of example input-output pairs are used to derive a function that can generate or predict new outputs from completely new inputs. That it, supervised learning has two main phases: training and predicting (transforming in our
case). The Fig. 1 shows both of them. During training, the input and output pairs from the dataset are used to “teach” the system until it learns. Once trained, we can give the ANN an input and it produces its corresponding output.
For the training phase, the dataset is split into three subsets: training, validation and test dataset. The training dataset contains most of the inputs-output pairs and is used to train the ANN (i.e., to adjust the weights of the ANN’s connections). The test dataset is only used once the training has finished to check the quality of the ANN’s predictions for inputs it has not seen before, and hence to study its accuracy (i.e., its correctness measured as the percentage of predictions our model gets right out of the total number of predictions).
The validation dataset plays a similar role but during the training process to control that the learning process is correct. More specifically, it is used to check that any accuracy increase over the training dataset also yields to an accuracy increase over the validation dataset. Otherwise (new training data does not result in improved accuracy), we say that the ANN is being overfitted. The overfitting is measured by means of the metric called validation loss.
3 Approach
This section introduces our approach. We first address the global architecture of the ANN framework we propose and then we talk about its potential configuration and the model pre- and postprocessing steps required to use the ANN in a model-based setting.
3.1 Global Architecture
Among all the artificial neural network family types and configurations [9] we have chosen Recurrent Neural Networks (RNN) as our subject of study. In RNNs, the neurons are organized in layers with forward connections (i.e., to neurons in the next layers) as well as back propagation connections (i.e.,
to neurons of the same layer or previous layers). This backpropagation mechanism in which the outputs of neurons are fed back into the network again makes the ANN “remember” some information from the previous step. This kind of neurons is called memory cells and make the ANNs be aware of their context. In our case, this kind of cells are helpful to remember, for instance, the name of a variable previously declared.
Long Short-Term Memory (LSTM) neural networks [10] are a specific kind of RNN which have a longer “memory” than their predecessors and are able to remember their context throughout different inputs. For instance, if we were transforming lines of code (one at a time), each line of code would be an input for the network. At some point in time, traditional RNNs would be able to remember only parts of the current input (line of code), while LSTMs are able to remember previous lines of code too. Clearly, in our transformation scenario, we may need this long-term memory to remember previous mappings as part of a more complex mapping pattern. Therefore, we have chosen LSTM neural networks as the most suitable networks to solve the problem of data transformation.
Nevertheless, after exhaustively testing a transformation architecture based on single LSTMs, we realized that not even LSTMs alone were enough to generate good results. Instead, we adopted a more complex framework based on an Encoder-Decoder [11] architecture that has been proven to be the most effective for dealing with translation problems.
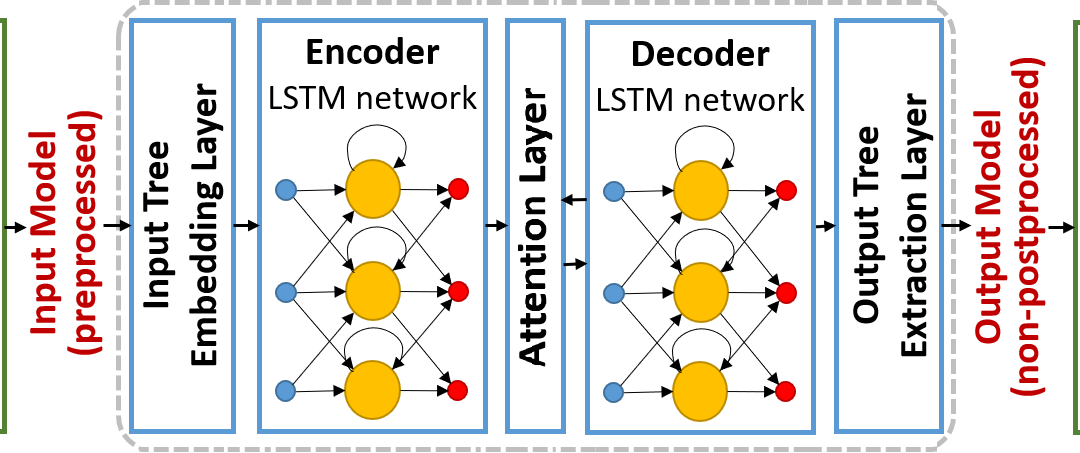
This architecture is composed of two RNN neural networks (of type LSTM in our case for the reasons described above): one that reads the input data (which is of variable size) and encodes it into a fixed-length numeric vector, and a second one that receives this vector and predicts (transforms in our case) the output data (which is again of variable size). In the literature, most of the works using this encoderdecoder architecture are applied to sequence-to-sequence transformations, for example, for natural language translation. In those cases, the raw input data that needs to be embedded is a sentence (i.e., a sequence of words). In our initial experiments, we found out this representation to be too simplistic since we were losing many of the structural information of the models. Therefore, we have settled for a more advanced tree-to-tree architecture (see Section 3.3). As a consequence, apart from the encoder and decoder, we need a layer to embed the input tree (representing the model after the preprocessing phase) into a format readable for the encoder. This input tree embedding layer is used to transform our input models in their tree-form into the numeric vectors which are the input to the LSTM encoder. We also need an output layer that takes the numeric vectors produced by the decoder and obtains the predicted (transformed) output model in its tree-form to be then passed on the postprocessing task to get the final output model. The output tree extraction layer does this.
Finally, our ANN architecture also includes an attention mechanism. Attention mechanisms applied to encoder-decoder architectures are placed as an intermediate layer between the encoder and the decoder. This layer allows the decoder pay more attention to specific parts of the fixed-size vector it
receives. This is, it allows the decoder to assign more value to specific parts of the model. The most important thing is that attention mechanisms are fully independent when it comes to deciding which parts of the input models are more important, i.e., they automatically learn to which parts the decoder has to pay more attention during the output model generation without any external guidance.
Fig. 2 shows inside the dotted box the complete picture of the ANN MT architecture described so far.
3.2 Configuration
All the components of our architecture have certain parameters that need to be configured to optimize the training phase depending on the specific problem they are going to solve. The core ones are the number of layers in each ANN, the number of neurons in each layer, the initial connection weights, the learning rate, the decay, the optimization algorithm, the dropout rate and the attention mechanism. Due to space limitations we cannot provide the full details of each parameter but we do show here the values we have used for them. Note that, users could change this default configuration if they wish but they can just use ours if they want to skip this configuration phase.
Both the encoder and decoder have one layer each with 256 neurons. The connection weights are initialized following a continuous uniform distribution on the interval [-1; 1]. The learning rate is 0.01 (i.e., the weights are updated a 1% in each iteration), with a decay of the 80% when the validation loss
does not decrease (i.e., when we detect that overfitting might be taking place). We have used the optimization algorithm Adam [12] to update parameters such as the weights to accelerate the convergence of the ANNs and thus, the training process. To avoid the overfitting, we have set a dropout rate of
0.5, which means that 50% of randomly selected the neurons are ignored in each iteration and thus, the weights of their connections will not be updated.
The embedding layer contains 256 neurons and receives the preprocessed models in its one-hot encoding representation. The output layer contains 256 neurons, too. The attention mechanism we use is the one proposed by Chen et al. in their work [13] for tree-to-tree translations.
3.3 Model pre- and post-processing
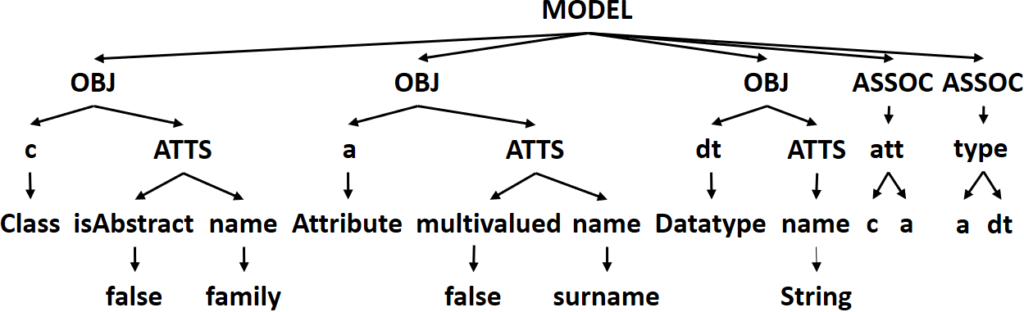
As said before, the models have to be preprocessed an represented as trees before being fed to the ANN. In the representation we have chosen, each model is represented as an independent tree. The root contains the keyword MODEL, and its children are the model elements, which can be either OBJECTSs or ASSOCIATIONs. Each object has a unique identifier which is represented as a child, and optionally, it has another child with the keyword ATTRIBUTES from where its attributes hang. Each attribute has two children with the attribute’s name and its value. Each association has two children, one with the name of the association (if there are more than two associations in the metamodel with the same name, they are automatically renamed first), and another child
with the keyword BETWEEN from where the two variables of the objects the association links. For simplicity, only binary associations are considered.
For instance, Fig. 3 shows a model and its tree representation. As a final step, these trees are encoded in a JSON file, which is the input to our program.
After converting the models to trees, we need to apply a normalization process to overtake two limitations that ANNs have.
The first one is what we call the dictionary problem. ANNs are able to “understand” only the words that are present in the dictionary that they build from the dataset. Thus, each word not present in the dictionary (i.e., not present in the models used for training) are not recognized by the network which treats them as the token UNK (short for unknown). Note that, when translating natural language, which is the most common use of the encoder-decoder architecture, this is not a problem since the dictionary contains all the words from the source and target languages. In our case, variable names and attribute values can be arbitrary string, which would make our dictionary infinite. To solve this problem, both for training and predicting transforming), we rename all variables and attribute values to a closed set of words. For instance: variables={A, B, C, D, E, …} and attValues={x, y, z, t, …}. Then, the models used for training only contain a minimum set of tokens which are known by the network. When predicting (transforming) new models, the inverse operation is performed as a postprocessing step to the output of the ANN to generate the proper output models with the right variable and attribute names.
The second one is an optimization to remove model symmetries, and thus, reduce the size of the training dataset. Given that we represent models as trees, a different ordering of the model elements in the tree would be considered by the ANN as a different input model and therefore it would require additional training. To avoid this, we remove potential symmetries by defining a canonical form for the tree-based model representation. In particular, right now we sort the model elements in alphabetical order according to its preorder traversal—in the future, we will explore how to deal with model symmetries with approaches such as [14]. Again, this task has to be done as a preprocessing step for every model both in the training and predicting phases.
4 Evaluation
We present a preliminary study of the results of our approach in terms of correctness and performance. To simplify the presentation, we use the well-known model transformation example Class2Relational [15].
The experiments have been executed in a machine with Ubuntu 16.04, an Intel i7 8th generation processor, 16Gb of RAM memory and no support for Nvidia CUDA. Note that using the GPU that an NVIDIA Graphic Card provides with CUDA usually speedups the training process and improves its scalability, but we felt that it was more realistic to assume that our target user would not have such specific equipment even if it is becoming more and more common.
4.1 Quality
As explained in Section 2, the correctness of ANNs is studied through its accuracy and overfitting (being the latter measured through the validation loss). The accuracy should be as close as 1 as possible while the validation loss as close to 0 as possible.
The accuracy is calculated comparing for each input model in the test dataset whether the output of the network corresponds with the expected output. If it does, the network was able to successfully predict/transform.
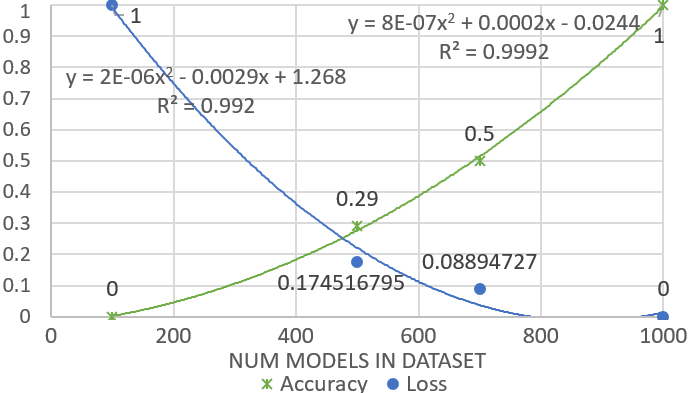
In Fig. 4 we show how the accuracy grows and the loss decreases with the size of the dataset, i.e., the more input-output pairs we provide for training, the better our software learns and predicts (transforms). In this concrete case, with a dataset with 1000 models, the accuracy is 1 and the loss 0 (meaning that no overfitting was taking place), which means that the ANNs are perfectly trained and ready to use. Note that we show the size of the complete dataset but, we have split it using an 80% of the pairs for training, a 10% for validation and another 10% for testing.
4.2 Performance
There are two performance dimensions we need to consider: how long does it take for the training phase to complete and; once the network has been trained, how long it takes to transform an input model with it. Note that the training needs to be performed only once per each transformation scenario.
Training performance
The two main factors that impact the training time are the size of the training dataset (i.e., the number of models that compose the dataset) and the average size of each models in it.
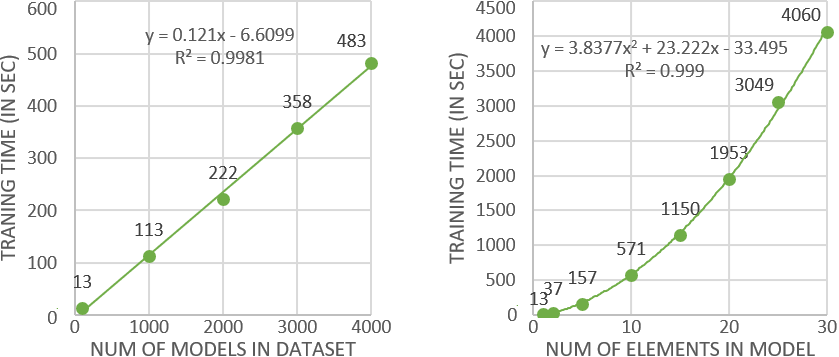
Fig. 5. Impact of the size of the training dataset (left) and of the size of the models (right) when training
Fig. 5 shows the performance of the training phase for the Class2Relational example depending on the size of the dataset and its models. On the left-hand side we can see how the training time grows linearly when increasing the size of the training dataset. Note that we were able to reach maximum accuracy for this example by using less models than those used in the figure (precisely we only needed 1000 as shown in Fig. 4) but we added additional ones to test its performance with more complex transformations. On the right-hand side we study the impact of growing the average size of the models. We have fixed the size of the training dataset to 100 pairs of input-output models and have varied the number of elements in each model (ranging from 1 to 30). As shown in the figure, there is a quadratic growth when increasing the size of the models. While this behaviour is worse than the former, it is less important as, based on our experiments, accuracy improvements are more linked to larger datasets than to larger models as ANN learn a lot by intensive repetition.
Transformation performance
After the training, we have evaluated the transformation time of the network on a set of input models and observed that the time grows linearly
with the number of model elements. As a reference, we have also compared the execution time of our ML-based transformation with the execution time of the
ATL version of the same transformation [15]. Thought ours was a little bit slower for the models we tested, time is within the same order of magnitude (less than a second for models up to 30 elements to be transformed) and, therefore, we do not see this as a negative aspect for ML-based transformations.
5 Replicability Package
To facilitate the replication of our study, we provide a Git repository for researchers interested in repeating or complementing our evaluations. The repository includes the source code, the trained ANNs, the model dataset used for training and the Java program that we have used to automatically
generate this dataset. It can be found here.
6 Discussion
We believe our results show that an ML-based approach for MT is feasible but obviously there are a number of open challenges to be solved before it can actually be used in practice. Here we discuss the main ones and provide potential ways to address them in the future.
- Size of the training dataset: ANNs require a considerable amount of data for training. In our case, this means that learning a model transformation may require a sizeable number of input-output models (the more complex is the transformation to learn, the more models are needed). While there is a number of model repositories available, finding enough model samples for a given domain is still clearly a challenge that could affect the quality of the results. Strategies to mitigate this issue would include data augmentation techniques (e.g., reusing model mutation procedures or employing Generative Adversarial Networks (GAN) [16] to generate further examples for a core set) or apply transfer learning [17] to avoid starting the learning process from scratch. Moreover, given the repetitive nature of many model transformations, pre-trained networks for typical transformation scenarios could be used instead as starting point to generate an optimal learning model for our use case with less training data required.
- Diversity in the training set: Related to the point above, the quality of the training is also tied to the diversity of the dataset. An ANN can only predict scenarios that follow a pattern that it has seen before. Coverage metrics for the input/output metamodels [18] and the use of graph kernel techniques [19] could give feedback to the user regarding the need for adding more samples to cover for corner cases.
- Computational limitations of ANNs: ANNs are still a field under heavy development with better learning continuously algorithms presented. However, as of today, they still have some limitations. One is their inability to perform mathematical operations. This implies our approach cannot predict values in the target model that should be the result of a mathematical computation of values from the input model. Given the importance of such a challenge in many domains, we are aware of several groups working on this issue and hope to see new developments soon.
- Generalization problem: ANNs are not good at generalizing and predicting output solutions for input models very different from the training distribution it has learned from. For instance, ANNs trained on small models typically have problems to predict well large models. This would require training the ANN with all possible model sizes for optimal results. This is not feasible so an alternative solution we have employed is to train the network with small models (also easier to find/generate) and, then, when faced with the need to predict larger ones split them in chunks, transform the chunks independently and then put the pieces back together again. Dependencies between the chunks may complicate this solution but note that this problem has already been successfully addressed for the parallel transformation of models [20].
- Social acceptance: Social factors may also hamper the adoption of a “black-box” ML-based transformation approach. Users may be reluctant to trust a piece of software that they are not able to understand. As done in other AI applications, adding explanation capabilities to the system will be a must.
- ML pipelines for MTs: One of the challenges we faced was putting in place the set of AI libraries and frameworks we needed and adapt them to understand, read and write models. We believe our platform and “model-based ML data pipeline” will, at the very least, facilitate follow-up works (by us or by other interesting researchers) in this area and speed up the ime it takes to prepare, run and evaluate ML experiments in MDE.
7 Related Work
The typical solution to tackle model transformation problems is to write a transformation program using a specific transformation language (e.g., just looking at the model transformation field we have plenty of well-known examples such as ATL, QVT and ETL). Still, the adoption of these languages in industry is limited. MT languages are not very intuitive to non-expert users and their IDEs usually lack the advanced facilities (e.g. nice debugging tools) required to develop transformations.
Model Transformation By-Example (MTBE) is an attempt to simplify the writing of exogenous model transformations [21]–[25]. In an MTBE approach, users have to provide source models, their corresponding target models as well as the correspondence between them—for which a correspondence language has to be used. From this, the MTBE approach generates partial mappings that form the basis of the transformation. Although these approaches free the user from learning a full transformation language, she has to still learn a correspondence language and manually build/complete the generated transformation mappings.
Kessentini et al. [26], [27] use search-based techniques to generate target models even if there is a limited number of examples available. The basic idea is to find among the examples the ones that are probably the closest match to the source model the user is trying to transform. Nevertheless, similar to the previous MTBE approaches they require the existence of transformation traces for the available examples so that they can generate the optimal solution.
Baki et al. [28] are able to discover more complex transformations by splitting the transformations traces in pools and applying genetic algorithms. Again, transformation traces are needed for the discovery phase.
In contrast to previous works, our approach does not require any kind of correspondence or tracing information to be provided by the user or domain expert and learns purely from the couples of input/output models. This enables non-expert users to employ our approach.
Model transformation is just an instantiation of the more general problem of data transformation, which shows up across many fields of computer science (e.g., databases, XML, modeling, and big data). This topic has been largely addressed by the (relational) database community, especially dealing with the
heterogeneity of the data sources and the impedance mismatch problems [29]–[31]. Nevertheless, ML-based approaches have not been attempted either in that community. We hope our results can be replicated in that context as well.
The programming research community has been much more active in the area of mixing ML and (code) transformation. In [13], Chen et al. use neural networks to translate code from one programming language to another. We have learn a lot from this work. Nevertheless, given that we transform models and not code, our work has adapted some of the ideas from [13] in several points such as the encoding for inputs and outputs, the need of a pre- and postprocessing steps and the parametrization of the neural networks to better fit the model transformation problem.
8 Conclusions and Future Work
In this paper, we have presented a ML architecture based on LSTM neural networks for automatically inferring MTs. We plan to continue this work along a number of different directions, mainly addressing some of the challenges discussed above. In particular, we plan to focus on the performance and usability of our approach (e.g. developing heuristics to help users configure and optimize the training phase, including recommendations on the size of the datasets) and study its applicability to similar domains (like model-to-text transformations). In parallel, we hope to collaborate with the model transformation community at large to better understand the role approaches like ours can play in the transformation domain. ML will not completely replace transformation languages but could make them redundant in a variety of scenarios. Better understanding the trade-offs of each transformation strategy (ML-based, by example, pure MTLs,…) would benefit us all.
REFERENCES
-
- K. Grace, J. Salvatier, A. Dafoe, B. Zhang, and O. Evans, “Viewpoint: When will AI exceed human performance? Evidence from AI experts,” J. Artif. Intell. Res., vol. 62, pp. 729–754, 2018.
- D. Lo Giudice, “How AI will change software development and applications,”https://www.nhaustralia.com.au/documents/AI_report.pdf.
- T. Xie, “Intelligent software engineering: Synergy between AI and software engineering,” in Proc. of ISEC’18, 2018, p. 1:1.
- J. Cabot, R. Clarisó, M. Brambilla, and S. Gérard, “Cognifying model-driven software engineering,” in Proc. of the Collocated Workshops @ STAF’17, 2017, pp. 154–160.
- M. Ibrahim and R. Ahmad, “Class diagram extraction from textual requirements using natural language processing (NLP) techniques,” in Proc. of the 2nd International Conference on Computer Research and Development, 2010, pp. 200–204.
- S. Pérez-Soler, E. Guerra, and J. de Lara, “Collaborative modeling and group decision making using chatbots in social networks,” IEEE Software, vol. 35, no. 6, pp. 48–54, 2018.
- V. Moreno, G. Génova, M. Alejandres, and A. Fraga, “Automatic classification of web images as UML diagrams,” in Proc. of CERI’16, 2016, pp. 17:1–17:8.
- Y. Wu, M. Schuster, Z. Chen, Q. V. Le, M. Norouzi, W. Macherey, M. Krikun, Y. Cao, Q. Gao, K. Macherey, J. Klingner, A. Shah, M. Johnson, X. Liu, L. Kaiser, S. Gouws, Y. Kato, T. Kudo, H. Kazawa, K. Stevens, G. Kurian, N. Patil, W. Wang, C. Young, J. Smith, J. Riesa, A. Rudnick, O. Vinyals, G. Corrado, M. Hughes, and J. Dean, “Google’s
neural machine translation system: Bridging the gap between human and machine translation,” CoRR, vol. abs/1609.08144, 2016. - J. Schmidhuber, “Deep learning in neural networks: An overview,”Neural Networks, vol. 61, pp. 85 – 117, 2015.
- S. Hochreiter and J. Schmidhuber, “Long short-term memory,” Neural Comput., vol. 9, no. 8, pp. 1735–1780, 1997.
- K. Cho, B. van Merrienboer, Ç. Gülçehre, D. Bahdanau, F. Bougares, H. Schwenk, and Y. Bengio, “Learning phrase representations using RNN encoder-decoder for statistical machine translation,” in Proc. of EMNLP’14, 2014, pp. 1724–1734.
- D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” in Proc. ICLR’15, Y. Bengio and Y. LeCun, Eds., 2015.
- X. Chen, C. Liu, and D. Song, “Learning neural programs to parse programs,” CoRR, vol. abs/1706.01284, 2017.
- A. Rensink, “Canonical graph shapes,” in Proc. of the ESOP’04, 2004, pp. 401–415.
- AtlanMod (Inria), “Class to relational transformation example,” https://www.eclipse.org/atl/atlTransformations/#Class2Relational.
- C. Bowles, L. Chen, R. Guerrero, P. Bentley, R. N. Gunn, A. Hammers, D. A. Dickie, M. del C. Valdés Hernández, J. M. Wardlaw, and D. Rueckert, “GAN augmentation: Augmenting training data using
generative adversarial networks,” CoRR, vol. abs/1810.10863, 2018. - E. S. Olivas, J. D. M. Guerrero, M. M. Sober, J. R. M. Benedito, and A. J. S. Lopez, Handbook Of Research On Machine Learning Applications and Trends: Algorithms, Methods and Techniques. Hershey, PA: Information Science Reference – Imprint of: IGI Publishing, 2009.
- O. Semeráth and D. Varró, “Iterative generation of diverse models for testing specifications of dsl tools,” in Proc. of FASE’18, 2018, pp. 227–245.
- R. Clarisó and J. Cabot, “Applying graph kernels to model-driven engineering problems,” in Proc. of MASES@ASE’18, 2018, pp. 1–5.
- L. Burgueño, M. Wimmer, and A. Vallecillo, “A linda-based platform for the parallel execution of out-place model transformations,” Information & Software Technology, vol. 79, pp. 17–35, 2016.
- G. Kappel, P. Langer, W. Retschitzegger, W. Schwinger, and M. Wimmer, “Model transformation by-example: A survey of the first wave,” in Conceptual Modelling and Its Theoretical Foundations: Essays Dedicated to Bernhard Thalheim on the Occasion of His 60th Birthday, 2012, pp. 197–215.
- D. Varró, “Model transformation by example,” in Proc. of MODELS’06, 2006, pp. 410–424.
- M. Wimmer, M. Strommer, H. Kargl, and G. Kramler, “Towards model transformation generation by-example,” in Proc. of HICSS’07, 2007, p. 285.
- I. García-Magariño, J. J. Gómez-Sanz, and R. Fuentes-Fernández, “Model transformation by-example: An algorithm for generating many-to-many transformation rules in several model transformation languages,” in Proc. of ICMT’09, 2009, pp. 52–66.
- Z. Balogh and D. Varró, “Model transformation by example using inductive logic programming,” Software and System Modeling, vol. 8, no. 3, pp. 347–364, 2009.
- M. Kessentini, H. A. Sahraoui, M. Boukadoum, and O. Benomar, “Search-based model transformation by example,” Software and System Modeling, vol. 11, no. 2, pp. 209–226, 2012.
- M. W. Mkaouer and M. Kessentini, “Model transformation using multiobjective optimization,” Advances in Computers, vol. 92, pp. 161–202, 2014.
- I. Baki and H. A. Sahraoui, “Multi-step learning and adaptive search for learning complex model transformations from examples,” ACM Trans. Softw. Eng. Methodol., vol. 25, no. 3, pp. 20:1–20:37, 2016.
- P. A. Bernstein and S. Melnik, “Model management 2.0: Manipulating richer mappings,” in Proc. of SIGMOD’07, 2007, pp. 1–12.
- J. F. Terwilliger, P. A. Bernstein, and A. Unnithan, “Automated coevolution of conceptual models, physical databases, and mappings,” in Proc. (ER’10), 2010, pp. 146–159.
- P. A. Bernstein, J. Madhavan, and E. Rahm, “Generic schema matching, ten years later,” in Proc. of VLDB’11, vol. 4, no. 11, 2011, pp. 695–701.
Lola Burgueño is an Associate Professor at the University of Malaga (UMA), Spain. She is a member of the Atenea Research Group and part of the Institute of Technology and Software Engineering (ITIS). Her research interests focus mainly on the fields of Software Engineering (SE) and of Model-Driven Software Engineering (MDE). She has made contributions to the application of artificial intelligence techniques to improve software development processes and tools; uncertainty management during the software design phase; model-based software testing, and the design of algorithms and tools for improving the performance of model transformations, among others.





Nice work!
Currently I am studying a new Neural Network architecture to deal with model transformation, is the dataset avaliable?.
On the other hand, I do not understand very well how you do to introduce the model to the NN. Is the code available?
Hi Pepe,
Yes, it is available. You can find both code and datasets here: https://github.com/modelia/ann-for-mts. I must say, though, that we have improved our solution. The work is not published yet but it will be soon.
L.
Thank you very much.
🙂