As part of my participation in the 12th Int. School on Formal Methods: Model-Driven Engineering I´ve co-authored an OCL tutorial book chapter (together with Martin Gogolla) introducing the Object Constraint Language (you may want to read why you need to learn OCL first).

The Object Constraint Language (OCL) started as a complement of the UML notation with the goal to overcome the limitations of UML (and in general, any graphical notation) in terms of precisely specifying detailed aspects of a system design. Since then, OCL has become a key component of any model-driven engineering (MDE) technique as the default language for expressing all kinds of (meta)model query, manipulation, and specification requirements. Among many other applications, OCL is frequently used to express model transformations (as part of the source and target patterns of transformation rules), well-formedness rules (as part of the definition of new domain-specific languages), or code-generation templates (as a way to express the generation patterns and rules). This OCL tutorial pretends to provide a comprehensive view of this language, its many applications, and available OCL tool support (including our own, python-based, OCL interpreter) as well as the latest research developments and open challenges around it.

And these are the slides I used during the tutorial (these slides have been seen over 110.000 times!)

The full text for this OCL tutorial can be found here but you can keep reading for a summary of the key sections, especially  targeting OCL beginners (all the rest go to the previous link for the more complete discussion):

1. Introduction to the Object Constraint Language tutorial

The Object Constraint Language  (OCL)  appeared as an effort to overcome the limitations of UML when it comes to precisely specifying detailed aspects of a system design. OCL was first developed in 1995 inside IBM as an evolution of an expression language in the Syntropy method [26]. The work on OCL was part of a joint proposal with ObjectTime Limited presented as a response to the RFP for a standard object-oriented analysis and design language issued by the Object Management Group  (OMG)  [26]. That standard came to be what we now know as UML and OCL became integrated in it in 1997.

Initially, OCL was only used as a constraint language for UML but quickly expanded its scope and now OCL has become a key component of any model-driven engineering (MDE)  technique as the default language for expressing all kinds of (meta)model query,  manipulation, and specification requirements. Among many other applications, OCL is frequently used to express model transformations (as part of the source and target patterns of transformation rules), well-formedness rules (as part of the definition of new domain-specific languages,  or code generation templates (as a way to express the generation patterns and rules).  To adapt the language to these new applications, several new (sub)versions of the language have been released. At the moment of writing this chapter, the current version of the OCL language is version 2.3.1 [20].

This chapter pretends to provide a comprehensive view of this language,  its many applications and available tool support as well as the latest research developments and open challenges around it. The rest of this chapter is structured as follows. Section 2 motivates the need for OCL. Section 3 gives a brief overview of the language,  while Section 4 provides a more precise language description. Then,  Section 5 classifies existing OCL tools. Finally,  Section 6 outlines a possible research agenda for OCL, and Section 7 provides some final conclusions.

2. Motivation: Why OCL is needed

Graphical modeling languages are the preferred choice for many designers when it comes to defining the structural aspects of a domain  (i.e.,  its  main concepts, their properties and the relationships between them). The most typical example of a graphical notation is UML [21], especially its class diagram  which is by far the most used UML diagram  [13].

Nevertheless, this facility of use comes with a  price.  In  order to keep the number of notational elements manageable, language designers must limit the expressiveness of the language.  This  means that graphical  notations can  only express  a  limited subset of all  the relevant information of a  domain.  This  is where OCL (and  in general,  any other textual language)  comes into play. They are a necessary complement of the UML (or other graphical  languages)  notation in order to be able to precisely specify all detailed aspects of a system design.

As an  example,  take  a look at the class diagram  of Figure  1 that will be used  as running example  throughout  the chapter.  This  diagram is an  excerpt of the EU-Rent  Car  Rentals  Specification  [14], an in-depth specification of the EU-Rent case study,  which is a widely known case study being promoted as a basis for demonstration of product capabilities. EU-Rent presents a car rental company with branches in several countries that provide typical rental services. EU-Rent was originally developed by Model Systems, Ltd.

This excerpt contains information about the rentals of the company  (Rental class), the company branches  (Branch class), the rented cars (Car ), the category to which they belong (CarGroup ) and  the customers (Customer ) that at some point in time may become blacklisted (BlackListed ) due to delayed  car returns, unpaid  rentals, etc. Each rented car has  one or more registered drivers  and  a pickup and drop off branch assigned.

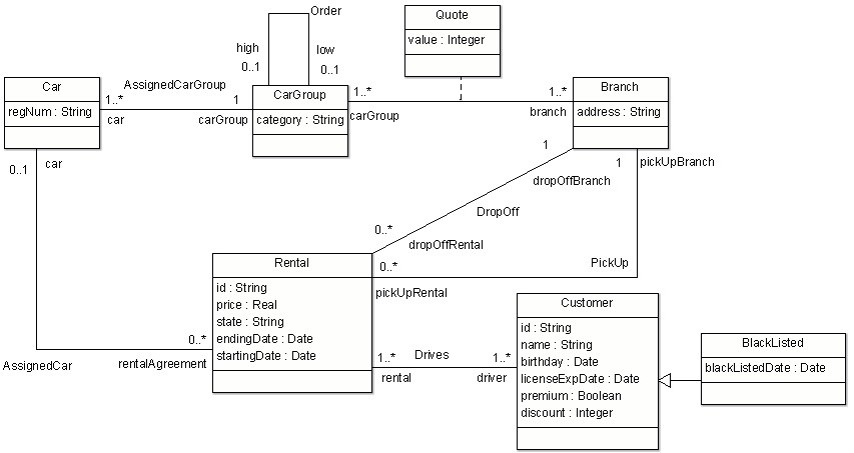
Fig. 1. Running Example – Partial Class  Diagram of the EU-Rent company

This may look like a quite complete definition of the problem but in reality, it is just the tip of the iceberg. Many important details cannot be defined just using the notation available for UML class diagrams.  Just to mention  some aspects that the UML diagram  does not answer:

1. Can blacklisted people rent new cars? (common sense may suggest answering no to this question but in fact, this is not specified anywhere in the diagram so different people may assume different answers)
2. How is the price of a rental calculated?
3. What are the conditions to be able to extend an existing rental?
4. Should the driving license of all drivers be valid throughout the full rental period? Is there a minimum driving seniority required?  Can the same driver have two active rentals?
5. Can the pickup and drop off branches differ?
6. Can I choose a car already assigned to another rental?

The next section will show how OCL can be used to express all these additional concerns.

3. OCL in  a Nutshell

The goal of this section is to give you an informal short description of the OCL and  show its usefulness by exemplifying how it can be used to solve the open questions left at the end of the last section.

OCL is a general-purpose (textual) formal language adopted as a standard by the OMG (see the current version of the OCL specification [20]) used to define several kinds of expressions that complement the information of (UML) models.

OCL is a typed, declarative and side-effect free specification language.  Typed means that each OCL expression evaluates to a type (either one of the predefined OCL types or a type in the model where the OCL expression is used) and must conform to the rules  and operations of that type. Side-effect  free  implies that OCL expressions can query or constrain the state of the system but not modify it.

Declarative means that OCL does not include imperative constructs like assignments. And finally, specification refers to the fact that the language definition does not include any implementation details nor implementation guidelines.

Among the many applications of OCL, it can be used to define the following kinds of expressions (for the sake of simplicity we focus on OCL usages in class diagrams) :

• Invariants to state all  necessary condition  that must be  satisfied  in each possible instantiation of the model.
• Initialization of class properties.
• Derivation rules that express how the value of derived model elements must be computed.
• Query  operations
• Operation contracts (i.e., set of operation pre- and postconditions)

In the following, we briefly introduce each expression type and explain some basic OCL construct along the way. The next section will present the full details of the language.

Invariants

Integrity constraints in OCL are represented as invariants defined in the context of a specific type, named the context type of the constraint. Its body, the boolean condition to be checked, must be satisfied by all instances of the context type.

Invariants are without a doubt the most common OCL expression since they allow designers to easily specify all kinds  of conditions that the system must comply with. Invariants can  restrict the value  of single objects, like the following QuoteOverZero :

context  Quote  inv  QuoteOverZero:  self.value  > 0

stating that all quotes must have a positive value. Note that the self variable represents an arbitrary instance of the Quote class and the dot notation is used to access the properties of the self object (as the value attribute in the example). As stated above,  all instances of Quote  (the content  type  of the constraint in this case) must evaluate this condition to true.

Nevertheless, many invariants express more complex conditions limiting the possible relationships between different objects in the system, usually related through association links.  For  instance, this NoRentalsBlackListed  constraint forbids BlackListed people from renting cars:

context  BlackListed  inv  NoRentalsBlackListed: self.rental->forAll(r  | r.startDate  < self.blackListedDate)

where we first retrieve all rentals linked to a blacklisted person and then we make sure that all of them were created before the person was blacklisted. This is done by iterating on all related rentals and evaluating the date condition on each of them; the forAll iterator returns true if and only if all elements of the input collection evaluate the condition to true.

Initialization  Expressions

OCL  can  be used to specify the initial value that the properties of an object must take upon the object creation. Obviously,  the type of the expression must conform to the type of the initialized property (this must also take into account cases where the property to be initialized is a collection).

For instance,  the following OCL  expression initializes  to false the value of the premium attribute of Customers (we are assuming that customers can only promote to the premium status after renting several cars).

context  Customer::premium:  boolean  init:  false

Derived Elements

Derived elements are elements whose value/population can be inferred from the value/population of other model elements as defined in the element’s derivation rule. OCL is a popular choice for specifying these derivation rules.

OCL derivation rules follow the same structure as init expressions (see above) although their interpretation is different. An init expression must be true when the object is created but the restricted property may change its value afterwards (i.e., customers start as non-premium but may evolve to premium during  their time in the system). Instead, derivation rules  constrain the value  of a derived element throughout all its life-span. Note that this does not imply that the value of a derived element cannot change,  it only means that it will always change according to the evaluation of its derivation rule.

As an example,  consider the following rule for the derived element discount in class Customer,  stating that premium members get a 30% discount while non-premium members get 15% if they have at least rented high category cars five times while the rest of the customers get no discount at all.

context  Customer::discount:  integer derive:
         if not  self.premium  then
            if self.rental.car.carGroup->select(c|c.category=’high’)->size()>=5 
            then  15 else  0  endif 
         else  30  endif

The select iterator in the expression returns the subcollection of elements from the input collection that satisfy the condition. Then,  the size collection operator returns the cardinality of the output subcollection and this value is compared with the ‘5’ threshold. Note that in this example, the input collection (self.rental.car.carGroup) is not a set but a bag (i.e., a collection with repeated elements) since a user may have rented the same car twice in different rentals or two cars belonging to the same car group.

Query Operations

Query  operations are  a wrapped  OCL  expression that queries the system data and returns the information to the user.

As an example, the following query operation returns true if the car on which the operation is executed is the most popular  in the rental system.

context  Car::mostPopular():  boolean
body:  Car::allInstances()->forAll(c1|c1<>self  
       implies c1.rentalAgreement->size()<=self.rentalAgreement->size())

Operation  Contracts

There  are two different approaches for specifying an operation effect: the imperative and declarative approaches  [27]. In an imperative specification, the designer explicitly defines the set of structural events (inserts/updates/deletes) to be applied when executing the operation. Instead, in a declarative specification,  a contract for each operation must be provided.  The contract consists of a set of pre- and postconditions.  A precondition defines a set of conditions on the operation input and the system state that must hold when the operation is issued while postconditions state the set of conditions that must be satisfied by the system state at the end of the operation. OCL is usually the language of choice to express pre- and postconditions for operation contracts at the modeling level.

As an  example,  the following newRental  operation  describes  (part of ) the business logic behind  the creation of a new rental in the EU-rent system:

context Rental::newRental(id:Integer, price:Real,  startingDate:Date, 
        endingDate:Date,  customer:Customer, carRegNum:String, pickupBranch:  Branch,  dropOffBranch: Branch)
pre:  customer.licenseExpDate>endingDate 
post: Rental.allInstances->one(r |  r.oclIsNew() and 
      r.oclIsTypeOf(Rental)  and r.endingDate=endingDate and  r.startingDate=startingDate 
      and r.driver=customer and  r.pickupBranch=pickupBranch  and r.dropOffBranch=dropOffBranch
      and r.car=Car.allInstances()->any(c | c.regNum=carRegNum))

The precondition checks that the customer has a valid license for the duration of the rental5  while the postcondition states that by the end of the operation a new object r  of type Rental must have been created and initialized with the set of values passed as parameters (note that postconditions are underspecifications, i.e., they only specify part of the system state at the end  of the execution which leads  to the frame problem  [4] and other similar issues;  this problem is not OCL-specific and thus it is outside of the scope of this chapter).

OCL Language Description

Figure  2 gives an overview of the OCL type system in form of a feature model. Using a tree-like description, feature models allow describing mandatory and optional features of a subject, and to specify alternative features as well as conjunctive features. In particular, the figure pictures the different kinds of available types. Before explaining the type system in a systematic way, let us discuss OCL example types that are already known or which can be deduced from the class diagram of our running example in Fig. 3.

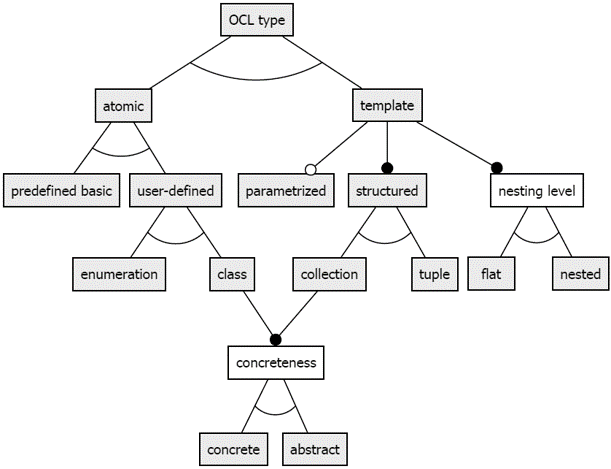
Fig. 2. OCL Types as a Feature Model

Attributes types, as for example in Car::regNum:String, are predefined basic, atomic types. Classes that are defined by the class diagram are atomic,  user-defined class types. If we already have an expression cg of type CarGroup, then the OCL expression  cg.car has the type Set(Car) due to the multiplicity 1..*. The type Set(Car) is a flat, concrete collection type. Set(Car) is a reification of the parametrized collection type Set(T) where T denotes an arbitrary type parameter that can be substituted. The type Sequence(Set(Car)) is a nested collection type being a reification of the parametrized, nested collection type Sequence(Set(T)). If cg:CarGroup is given,  then the expression  Tuple{cat:cg.category,  cars:cg.car} has  type Tuple(cat:String,  cars:Set(Car)) which is a tuple type.

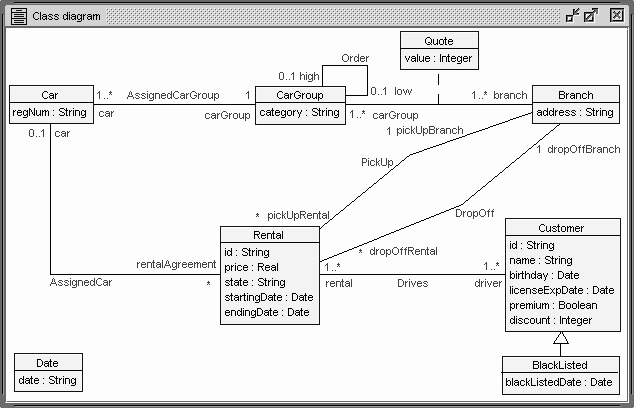
Fig. 3. Example Class Diagram in USE tool

Jordi Cabot

FNR Pearl Chair. Head of the Software Engineering RDI Unit at LIST. Affiliate Professor at University of Luxembourg.  More about me.