Machine Learning (ML) can be used to analyze and classify large collections of graph-based information, e.g. images, location information, the structure of molecules and proteins, . . . Graph kernels is one of the ML techniques typically used for such tasks.

In a software engineering context, models of a system such as structural or architectural diagrams can be viewed as labeled graphs. Thus, as part of our cognification of model-driven engineering initiative, we propose to employ graph kernels for clustering software modeling artifacts. Among other benefits, this would improve the efficiency and usability of a variety of software modeling activities, e.g., design space exploration, testing or verification and validation.

This work will be presented at the 1st International Workshop on Machine Learning and Software Engineering in Symbiosis. Keep reading to learn more about our application of Graph Kernels to solve software modeling problems!

INTRODUCTION

Model-Driven Engineering (MDE) [8] is a software engineering paradigm that advocates the use of models as central artifacts of the software development process. Designers use models to describe the structure, features, architecture and behavior of a software system, using notations such as UML or SysML. Then, model transformations are used to manipulate models for a variety of tasks, e.g. generating code for the final implementation of the software system.

Focusing on models instead of source code allows designers to work at a higher-level of abstraction, postponing implementation- specific decisions until later development stages. Indeed, activities such as validation, verification or testing can be performed at the model level, provided that suitable tool support is available to designers.

Some of these activities require dealing with large collections of models that describe a system from the same perspective. These models may be built either by hand or generated automatically (through model transformations, constraint solving, . . . ). An exam- ple would be the generation of model instances to be used as test cases or as examples for validation purposes.

From the perspective of tools, managing such collection of mod- els can be challenging. Designers would greatly benefit from the ability to organize these collections of models, e.g. being able to identify clusters of similar models. Rather than working with the entire collection, designers could instead work with one represen- tative model from each cluster. In this way, several modeling activi- ties would become more usable and more efficient, due to a lower cognitive load and having less data to be manipulated. Moreover, designers would be able to measure and enforce model diversity [11, 18], i.e. check that a model collection includes models with distinct features rather than many almost identical copies.

While in MDE there are some graph-based solutions with these goals, they are problem specific. We believe that methods inspired by Machine Learning (ML), and in particular graph kernel methods for clustering, can provide a general framework that is useful in a wide variety of MDE tasks. In this paper, we describe graph kernels and propose their application to a variety of problems in the context of MDE.

The remainder of this paper is structured as follows. Section2 explains the concept of graph kernel. Then, Section3shows how it can be applied in MDE and discusses potential MDE problems and lines of research where we envision that the use of graph kernels can be specially useful. Section4discusses related work on graph kernels and its application to software engineering problems in MDE. Finally, Section5concludes and discusses potential lines of future work.

GRAPH KERNELS

Graph-based information in Machine Learning scenarios can appear in two different forms [4]. First, problem data can form a single very large graph where the challenge is identifying relevant subgraphs [22, 29]. On the other hand, data can be a collection of instances, where each instance is a separate graph [21, 28]. In MDE, both the models describing the system being developed (e.g., a class diagram) and the instantiations of these models (e.g., in the form of an object diagram) can be viewed as a graph. We believe that many MDE- related tasks could benefit from analyzing these graphs in order to compare them, study their characteristics and differences and then take advantage of this information. Therefore, in this paper we focus on this second scenario: studying a collection of graphs.

In this context, ML offers two approaches to analyze graph-based information:

• Vector-space embedding [21]: Encode each graph into a vector of features of a fixed
• Graph kernel [12,28]: Define a distance metric among each pair of

Vector-space embedding is not a single method, but rather a family of methods, as there are many ways in which features can be selected from a graph. The accuracy of the solution will greatly depend on the choice of features in our embedding. There are even approaches that attempt to learn suitable embeddings without the need of human supervision [14].

Similarly, graph kernels also constitute a family of methods rather than a single approach, given the many potential metrics for the distance between two labeled graphs. Kernels usually work around three concepts [24]: walks or paths (sequences of nodes in a graph); graphlets (subgraphs of a limited size); and subtree patterns (acyclic subgraphs). The distance is defined by counting the number of equivalent substructures (walks, subgraphs or subtrees) in both graphs. More recent works like propagation kernels [12] add new capabilities such as dealing with incomplete information, e.g. missing labels in the graph.

There is no single “best” graph kernel, as each one is more suitable for a particular type of problem. Moreover, each method has several parameters to customize the algorithm, which may affect the computation time and/or the accuracy of the distance metric being computed. Efficiency is usually polynomial over the number of nodes and/or edges, with a low exponent being key to remain usable in problem domains with large graphs.

Note that vector space-embeddings can be regarded as closely related to graph kernels. For example, a possible distance metric between two graphs can be defined as “compute a feature vector for both graphs and compute the distance between both feature vectors”. Nevertheless, in the context of MDE graph kernels offer several advantages with respect to vector-space embeddings:

• Graph kernels are better at taking into account the structure of a graph, rather than a few salient characteristics.
• Graph kernels do not require selecting a finite (and fixed) set of features, what is known as the kernel trick.

For these reasons, graph kernels are easier to apply to new problems that depend on the structure of the graph, as less effort is required to select the right set of features.

 

SOLVING MDE PROBLEMS WITH GRAPH KERNELS

Overview

In this Section, we explain how to apply graph kernels to analyse models of a software system. Graph kernel algorithms operate on a collection of N labeled graphs and produces a N × N kernel matrix where each cell (i, j) is a metric of the distance between graphs i and j. Starting from a collection of models, the following steps need to be followed:

1. Decide how the model should be encoded into a graph: which elements will become vertices, which ones will become edges and how labels will be assigned to both vertices and edges (g., encoding the type or value of the modeling element). Some algorithms (or their implementations) require labels to be numeric values rather than strings, so it may be necessary to assign numeric ids to strings.
2. Translate each of the models into a labeled graph. For example, we can use a model-to-text transformation to generate a graph description in a textual format such as GML or GraphML.
3. Select the graph kernel algorithm to be used. The “best” algorithm will depend on two factors: the particular problem being studied (as it establishes which graph substructures are relevant) and the size of the models under analysis (as some kernel algorithms are more efficient than others). As there is no clear recipe to select the best algorithm for a new problem, most works using graph kernels evaluate several algorithms using a representative dataset, selecting the one with the best accuracy/efficiency trade-off.
4. Load all the graphs and compute the graph kernel. Some libraries like igraph [3] support the management of graphs and other libraries such as the graphkernels package [27] (available for R and Python) offer implementations for the most common types of
5. Exploit the information in the kernel matrix. This information can be used directly, g. searching the matrix to find the most similar graph to a given one, or as part of a larger model processing pipeline, e.g. as the input of a clustering algorithm to group the graphs or a classification algorithm to predict properties of interest.

Applications

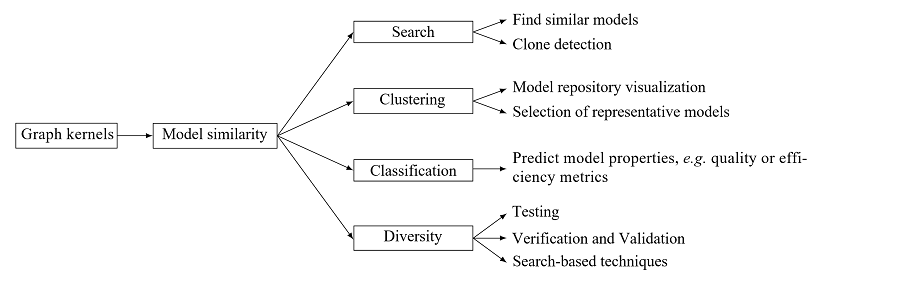
In this Section, we discuss potential areas of application of graph kernels in the context of MDE. A graph kernel offers a measure  of similarity (or dissimilarity), which can be used in a variety of ways. As presented in Figure1, we envision four major areas of application: diversity, search, clustering and classification.

Search

A similarity metric among models can be used as a mechanism to find similar models in a model repository. This search can have a variety of applications:

• In a model repository, it is possible to identify models with a similar structure. This can help a user navigate a model repository, detect clones (equal or almost equal models) or even reuse or adapt modeling assets (e.g. model transformations) from projects with a similar structure.
• In an educational setting, when considering modeling activities where students have to design a model for a system (e.g., given a list of textual requirements), it is possible to find similar exercises in a collection. In this way, if a student is having problems with a particular type of exercises, we can recommend similar exercises for him to practice.

Clustering

Given a collection of models, graph kernels can be used to perform clustering to identify groups of related models (clusters). In order to reduce the computational effort or cognitive load required to handle the entire collection, it would be possible to use representative models from each cluster, ensuring that all families of similar models are considered in the analysis.

Verification and validation. Verification and validation (V&V) tools for MDE provide a way to check whether specific properties are satisfied by a given model [9, 13]. Rather than a simple “yes” or “no”, the answer provided by V&V tools includes examples or counterexamples of the property under analysis, such as instantiation of the models, traces, . . . In addition to validating the original model, these outputs can also be used in other ways, such as test data.

Nevertheless, the primary concern of verification tools is their expressive power (which properties can be checked) and efficiency (how fast it can respond and how scalable it can be for larger models). This means that V&V tools suffer from usability problems. In particular, V&V tools tend to offer little support in terms of guiding the output (with a few notable exceptions [19, 23]). This means that in most V&V tools it is not possible to request that the output (counter)examples are similar or distinct from a given example, or among themselves if the tool is invoked repeatedly.

In this domain, kernel methods can be used to organize outputs produced by V&V tools into clusters, facilitating their visualization and comprehension; or reduce large sets of examples by choosing representatives from each cluster.

Design space exploration. Models can be used at an early stage of software development to gain a better understanding on the system under construction. At this level, examples and alternative to design decisions play a very important role [20].

In this context, similarity metrics can be used to navigate a collection of design alternatives efficiently, by visualizing the similarities among several solutions.

Classification

In some problem domains, the structure of a model may be correlated with some relevant properties of the final software implementation: development effort, defect rate, maintainability, . . .

Thus, given a large collection of models labeled with a set of characteristics, techniques such as support vector machines (SVM) can take advantage of the kernel matrix to learn how to classify new models based on their structure. That is, we could train a SVM to predict the characteristics of new models. While these approaches have been applied at the source code level [10], they can also be studied at the model level.

Diversity

Given a model (our input) and a collection of models, the graph kernel can be used to discard models in the collection which are too similar to the input. This analysis can be applied in an existing collection of models or while the collection is being generated, pruning too similar models before they are considered.

Verification and validation. As mentioned before, verification and validation tools may provide large collections of sample instances that need to be organized. Kernel methods can ensure diversity by choosing dissimilar models, avoiding examples which are too repetitive with respect to previously computed solutions. This filtering of too similar solutions can be performed during the search for of solutions or a posteriori, when a set of potential solutions is available.

Testing. A test suite can include a large number of (potentially redundant) test cases, which in the context of object-oriented pro- grams may involve a complex collection of potentially interrelated objects (i.e. a labeled graph) as the input. There is a large body of literature devoted to test-suite reduction [25], i.e. the elimination of redundant test cases from a test suite according to some criteria.

Typical criteria for test-suite reduction include coverage. However, these approaches do not typically consider the similarity among test cases. In the context of object-oriented programs, kernel methods may provide a mechanism to identify similar test inputs and use this information to guide test-suite reduction, that is, “remove similar tests first”.

Search-based techniques. Search-based methods often generate new solutions by visiting neighbors of existing solutions, e.g. introducing changes or combining different solutions. Graph kernels can provide a distance metric to make sure that new solutions differ sufficiently from existing ones before exploring them, or forbidding changes that do not alter the model structure significantly.

RELATED WORK

In this Section, we describe works considering the similarity of models in the context of Model-Driven Engineering. There are three major areas of application: model comparison, model clustering and model diversity.

Model Comparison

A broad range of techniques have been applied to compare pairs of models highlighting the similarities and differences among them [16, 26], with tools such as EMF Compare [1] or EMF Diff/Merge [2]

. These techniques can be used for a wide variety of goals: model merging [5], model versioning [15], testing of model transforma- tions [17], . . .

These approaches are oriented to work on a single pair of models and aim to produce computations equivalent to the graph edit distance or graph isomorphism. Therefore, they produce results which can be more precise than that of graph kernel methods. Nevertheless, kernel based methods are more efficient and can deal with collections of models beyond pairs.

Model Clustering

Another area of application is the classification of models in a model repository into clusters of similar models using vector space embeddings [6, 7]. The produced clusters are used to organize model repositories, providing overviews and visualizations to facilitate browsing and search.

Model Diversity

A final area of application of similarity consists on ensuring the diversity of a collection of models by making sure that models are dissimilar enough.

Dissimilarity can be enforced during the computations of instances of a model, for example in the Alloy relational solver [19] (by ensuring the minimality of the solution models) or the graph- based solver Viatra [23] (by using neighborhood graph shapes). On the other hand, another approach [11] measures similarity using a vector-space embedding. This similarity can be used to visualize distances among models, detect clones, select dissimilar models in an existing collection or generate dissimilar models through a genetic algorithm.

Recap

Few works have considered the application of Machine Learning techniques to address the MDE challenges dicussed in Figure1, and are based on the use of feature vectors. Nevertheless, graph kernels are better at considering the structure of the graph and do not require the same amount of fine tuning (i.e., feature selection) to be successful. Thus, we claim the application of graph kernels to MDE can solve relevant problems and provide benefits with respect to existing solutions for similar tasks.

CONCLUSIONS AND FUTURE WORK

In this paper, we have proposed the use of graph kernels as a general framework for approaching problems in Model-Driven Engineering. Graph kernels can improve the usability and efficiency of different software engineering tasks involving models, such as design space exploration or verification, validation and testing.

One particular advantage of this approach is the availability of efficient libraries performing graph operations and computing graph kernels that can be easily adapted to deal with graphs representing software models. Therefore, there is no need to reinvent the wheel or to reimplement existing methods from the literature.

As immediate future work, it is important to identify the most suitable kernel for each type of MDE problem and, possibly, for each kind of model. While predefined kernel algorithms provide good results, we believe taking into account the specific semantics of each model type in order to provide specialized distance functions could optimize the quality of the results when needed. Moreover, we plan to integrate existing graph kernel algorithms and packages with modeling technologies like EMF to make these techniques easily available for the modeling community at large.

REFERENCES

1. [n. d.]. EMF Compare.https://www.eclipse.org/emf/compare/.
2. [n. d.]. EMF Diff/Merge.https://www.eclipse.org/diffmerge/.
3. [n. d.]. igraph – The network analysis package.http://igraph.org/.
4. Charu C. Aggarwal and Haixun Wang. 2010. A Survey of Clustering Algo- rithms for Graph Data. Springer, Boston, MA, 275–301.https://doi.org/10.1007/ 978-1-4419-6045-0{_}9
5. Wesley G. Assunção, Silvia R. Vergilio, and Roberto E. Lopez-Herrejon. 2017. Discovering Software Architectures with Search-Based Merge of UML Model Variants. In ICSR 2017: Mastering Scale and Complexity in Software Reuse. Springer,Cham, 95–111.https://doi.org/10.1007/978-3-319-56856-0{_}7
6. Onder Babur and Loek Cleophas. 2017. Using n-grams for the Automated Clus- tering of Structural In SOFSEM 2017: Theory and Practice of Computer Science. Springer, 510–524.https://doi.org/10.1007/978-3-319-51963-0{_}40
7. Francesco Basciani, Juri Di Rocco, Davide Di Ruscio, Ludovico Iovino, and Alfonso Pierantonio. Automated Clustering of Metamodel Repositories. In CAiSE 2016: Advanced Information Systems Engineering. Springer, Cham, 342–358
8. Marco Brambilla, Jordi Cabot, and Manuel 2012. Model-Driven Software Engineering in Practice. Vol. 1. Morgan & Claypool Publishers. 1–182 pages.
9. Cabot, R. Clarisó, and D. Riera. 2014. On the verification of UML/OCL class dia- grams using constraint programming. Journal of Systems and Software 93 (7 2014), 1–23.http://www.sciencedirect.com/science/article/pii/S0164121214000739
10. Karim O. Elish and Mahmoud O. Elish. 2008. Predicting defect-prone software modules using support vector Journal of Systems and Software 81, 5 (5 2008), 649–660.https://doi.org/10.1016/j.jss.2007.07.040
11. Adel Ferdjoukh, Florian Galinier, Eric Bourreau, Annie Chateau, and ClÃľmentine Nebut. Measuring Differences to Compare sets of Models and Improve Diver- sity in MDE. In ICSEA, International Conference on Software Engineering Advances. http://adel-ferdjoukh.ovh/wp-content/uploads/pdf/icsea17-distances-v9.pdf
12. Swarnendu Ghosh, Nibaran Das, Teresa Gonçalves, Paulo Quaresma, and Mahan- tapas 2018. The journey of graph kernels through two decades. Computer Science Review 27 (2 2018), 88–111.https://doi.org/10.1016/J.COSREV.2017.11.002
13. Carlos A. González and Jordi Cabot. Formal verification of static soft- ware models in MDE: A systematic review. Information and Software Technol- ogy 56, 8 (8 2014), 821–838.http://www.sciencedirect.com/science/article/pii/ S0950584914000627
14. Aditya Grover and Jure 2016. node2vec: Scalable Feature Learning for Networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.http://arxiv.org/abs/1607.00653
15. Timo Kehrer, Udo Kelter, and Gabriele Taentzer. 2013. Consistency-preserving edit scripts in model In 2013 28th IEEE/ACM International Conference on Automated Software Engineering (ASE). IEEE, 191–201.https://doi.org/10. 1109/ASE.2013.6693079
16. Dimitrios S. Kolovos, Davide Di Ruscio, Alfonso Pierantonio, and Richard F. Paige. Different models for model matching: An analysis of approaches to support model differencing. In 2009 ICSE Workshop on Comparison and Versioning of Software Models. IEEE, 1–6.https://doi.org/10.1109/CVSM.2009.5071714
17. Yuehua Lin, Jing Zhang, and Jeff 2005. A Testing Framework for Model Transformations. In Model-Driven Software Development. Springer-Verlag,Berlin/Heidelberg, 219–236.https://doi.org/10.1007/3-540-28554-7{_}10
18. Meiyappan Nagappan, Thomas Zimmermann, and Christian 2013. Diversity in software engineering research. In Joint Meeting of the European Software Engineering Conference and the ACM SIGSOFT Symposium on the Foundations of Software Engineering. ACM Press, New York, New York, USA, 466.
19. Tim Nelson, Salman Saghafi, Daniel J. Dougherty, Kathi Fisler, and Shriram Krishnamurthi. 2013. Aluminum: Principled scenario exploration through mini- In 2013 35th International Conference on Software Engineering (ICSE). IEEE, 232–241.https://doi.org/10.1109/ICSE.2013.6606569
20. David Notkin, Betty C. Cheng, Klaus Pohl, MichaÅĆ IEEE Computer Society., Institute of Electrical, Zinovy Electronics Engineers., Andrzej W¸asowski, and Derek Rayside. 2013. Example-driven modeling: model = abstractions + examples. In Proceedings of the 2013 International Conference on Software Engineering. IEEE Press, 1273–1276.https://dl.acm.org/citation.cfm?id=2486982
21. Kaspar Riesen and Horst 2009. Graph classification based on vector space embedding. International Journal of Pattern Recognition and Artificial Intelligence 23, 06 (9 2009), 1053–1081.https://doi.org/10.1142/S021800140900748X
22. Satu Elisa Schaeffer. 2007. Graph clustering. Computer Science Review 1, 1 (8 2007), 27–64.https://doi.org/10.1016/J.COSREV.2007.05.001
23. OszkÃąr Semeráth and DÃąniel Varró. 2018. Iterative Generation of Diverse Models for Testing Specifications of DSL In FASE 2018: Fundamental Ap- proaches to Software Engineering. Springer, Cham, 227–245.https://doi.org/10. 1007/978-3-319-89363-1{_}13
24. Nino Shervashidze, Pascal Schweitzer, Erik Jan van Leeuwen, Kurt Mehlhorn, and Karsten Borgwardt. 2001. Weisfeiler-Lehman Graph Kernels. The Journal of Machine Learning Research 12 (2001), 2539–2561.https://dl.acm.org/citation. cfm?id=2078187
25. August Shi, Alex Gyori, Milos Gligoric, Andrey Zaytsev, and Darko Marinov. 2014. Balancing trade-offs in test-suite In Proceedings of the 22nd ACM SIGSOFT International Symposium on Foundations of Software Engineering – FSE 2014. ACM Press, New York, New York, USA, 246–256.https://doi.org/10.1145/ 2635868.2635921
26. Matthew Stepahn and James R. Cordy. 2013. A Survey of Model Comparison Approaches and Applications. In Proceedings of the 1st International Conference on Model-Driven Engineering and Software Development. SciTePress – Science and and Technology Publications, 265–277.https://doi.org/10.5220/0004311102650277
27. Mahito Sugiyama, M Elisabetta Ghisu, Felipe Llinares-López, and Karsten Borg- wardt. 2018. graphkernels: R and Python packages for graph comparison. Bioin- formatics 34, 3 (2 2018), 530–532.https://doi.org/10.1093/bioinformatics/btx602
28. V.N. Vishwanathan, Nicol N. Schraudolph, Risi Kondor, and Karsten M. Borg- wardt. 2010. Graph Kernels. Journal of Machine Learning Research 11, Apr (2010), 1201–1242.http://www.jmlr.org/papers/v11/vishwanathan10a.html
29. Yang Zhou, Hong Cheng, and Jeffrey Xu Yu. 2009. Graph clustering based on structural/attribute Proceedings of the VLDB Endowment 2, 1 (8 2009), 718–729.https://doi.org/10.14778/1687627.1687709