The structure and behavior of a software system can be described by means of software models, using notations such as Alloy, graph-based formalisms or UML/OCL. These notations describe software systems at a high level of abstraction, hiding implementation details while preserving its salient features. Analyzing these models can reveal complex faults in the underlying systems.
In this analysis, the key assets for checking the correctness of software models are model finders, tools capable of computing instances of a model that satisfy a set of constraints and properties of interest. Each model finder targets a particular modeling notation and uses a different reasoning engine, like search-based methods, SAT, SMT or constraint programming.
For verification purposes, it is usually enough to search for one instance, which either proves or disproves the property of interest. However, for testing and validation purposes several instances are usually required to increase our confidence in the correctness of the model. It is highly desirable that those instances exhibit diversity, i.e., distinct configurations of the system and interesting corner cases. Lack of diversity may make the validation and testing more time-consuming, as the analysis includes almost-duplicate instances that do not provide added value; and less effective, as the sample of instances may fail to include relevant scenarios.
Nevertheless, most model finders focus on efficiency and expressiveness of the input modeling notation, so few of them ensure the diversity of the generated instances. In these few, diversity assurance is integrated into the solver: it guides the search process to look for diverse instances. However, this integration makes it harder to transfer the proposed methods to other solvers and notations. Thus, designers are limited in terms of expressiveness (e.g., no support for integer or string attributes or dynamic properties) and cannot benefit from additional features provided by others model finders (e.g., computation of minimal instances or support for max-satisfiability).
We propose a method for distilling diverse instances in the model finder output based on the use of clustering. Instances are classified into categories according to their similarity, which is calculated using information about their structure (the existing objects and the links between them), typing (the specific type of each object) and attribute values depending on a custom definition that can be specified using a new domain-specific language we created for this purpose. This calculation is based on the use of graph kernels (see other potential benefits of using graph kernels in a variety of model-driven engineering problems), a family of methods for computing distances among graphs. Selecting a representative instance from each category ensures diversity while reducing testing and validation time, as redundant instances can be safely discarded. As a drawback, this method does not force the model finder to look for diverse instances, it only distills from those generated the most diverse ones.
Compared with related works, our approach offers the following advantages:
- It is independent of the solver used by the model finder (SAT, SMT, …) and the modeling notation being analyzed (Alloy, UML/OCL, …).
- It does not require manual intervention from the designer to define what kind of instances are \relevant” or when two instances are \similar”.
- The similarity computation can be customized, e.g., by selecting a trade-off between precision and accuracy.
So to sum up, the main highlights of our approach could be summarized as:
- Achieving diversity in example instances is a challenge for model finders.
- Current limitations include: lack of customization and solver-specific methods.
- We propose a method based on clustering and graph kernels to identify diverse instances of a model.
- The proposed method is completely decoupled from the verification algorithm.
- A domain-specific language lets designers customize the notion of diversity.
A first version of this work was accepted at ABZ 2020 (7th International Conference on Rigorous State-Based Methods). You can read the full paper Diverse scenario exploration in model finders
using graph kernels and clustering and an extended version has just appeared in the Science of Computer Programming journal, you can read this new version for free: “User-driven diverse scenario exploration in model finders” or keep reading for an overview.
Overview of our diversity method
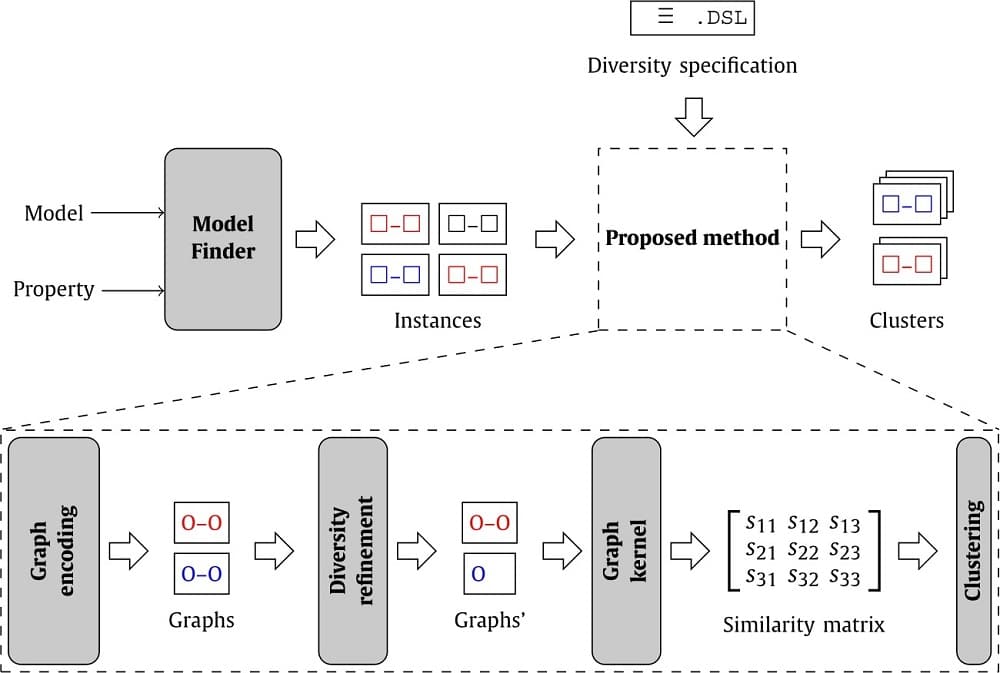
The overview of our approach for identifying diverse instances in model finder output is depicted in the featured image above. Our input is a set of instances computed by a model finder, and our output is a set of clusters grouping those instances according to their similarity. From this output, it is possible to select a representative instance for each cluster, e.g., choosing the smallest instance.
The method can be divided into four steps:
- Graph encoding: First, each instance is abstracted as a labeled graph, where labels store type and attribute value information and the underlying graph captures the objects and the links among them.
- Diversity refinement: The information in the labeled graph is filtered, aggregated and abstracted to meet the diversity specification provided by the user. This is an optional step: if no specification is given, the default graph encoding is not modified.
- Graph kernel: Then, the pairwise similarity among the n graphs is computed using a state-of-the-art labeled graph comparison technique. The result of this computation is a symmetric matrix S where each cell measures the similarity between graphs i and j. This notion of similarity measures repeated structures between the two graphs (i.e., matching labels and connectivity patterns). Thanks to our graph encoding, which stores type and attribute value information as labels, this means that our similarity metric is implicitly considering types, values and topological information simultaneously.
- Clustering: Finally, the similarity data is used by a clustering procedure to classify instances into groups of similar instances. The most suitable number of groups is determined by using clustering validity indices, which measure whether elements in the cluster are similar to each other and different from elements in other clusters.
Graph encoding
Our method for improving diversity aims to support different modeling notations and model finders, as well as taking advantage of off-the-shelf graph comparison algorithms. Thus, we need to translate the instances generated by the model finders for a given modeling scenario into labeled undirected graphs.
We specially focus on describing the encoding process for Alloy.
Customizing diversity
we propose a domain-specific language that designers can use to select and refine the model features that are important for them when determining the level of diversity. Using this DSL, designers can specify the submodel of interest or aggregate some properties of the elements in the model. Any information from the instance outside this submodel is still generated by the model finder, but it is filtered out when it comes to measuring and enforcing diversity among instances.
This DSL aims to be concise, usable and expressive. It offers high-level concepts that will be familiar to designers rather than implementation details such as the distance function being used. The language comprises a set of modeling primitives in order to:
- Define the signatures, relations and attributes that are relevant from a diversity perspective, i.e., all others can be ignored.
- Identify the fields whose values can be abstracted, i.e., it is not necessary to consider their specific individual value. Instead, we would like that value to satisfy a diversity of properties of interest or to fall within different categories according to some criteria.
- Specify the information in a relation that is only relevant in an aggregate form, e.g., count the number of objects participating in the relation or compute the sum/min/max of a numeric attribute.
Graph Kernels
Graph Kerrnels are a family of methods for measuring the (dis)similarity among pairs of graphs. Rather than computing an exact measure for similarity, kernels aim to provide an efficient approximation that can be computed efficiently but still captures relevant topological information about the graphs. A typical approach is counting the number of matching substructures within the graphs, like paths, subtrees or subgraphs.
In this work, we have used the Weisfeiler-Lehman kernel.
Clustering
Clustering is one of the fundamental tasks in the field of Machine Learning (ML). Intuitively, it consists in the analysis of a collection of elements to identify groups of similar individuals, for a given definition of “similarity”. There is no single “best” clustering algorithm: the most suitable one depends on the collection being analyzed.
In our context, the elements we are trying to cluster are labeled graphs abstracting the outputs of a model finder. The number of target clusters is unknown a priori. Moreover, the graphs to be clustered are not described as a feature vector: instead, the similarity metric provided by the Weisfeiler-Lehman graph kernel is used to compare them. The lack of a feature motivates us to select a hierarchical clustering method, in particular using a bottom-up or agglomerative strategy (by merging the two most similar clusters in the current level)
Putting it all together
To illustrate how the method works and the type of results it can achieve, we will use the following UML class diagram (Fig 1. section a). This model describes the relationships between employees who work in or lead a department. There are two constraints regarding the salary, defined as OCL invariants: all salaries must be below a salary threshold and also below the salary of the department’s director.
To be usable in practice, this model should be strongly satisfiable: it should have some instance where all integrity constraints are satisfied with each class having a non-empty population. In our example, the class diagram is satisfiable and a potential solution is the instance shown in Fig 1. section b. Instances like this can then be used for validating and testing the UML/OCL model.
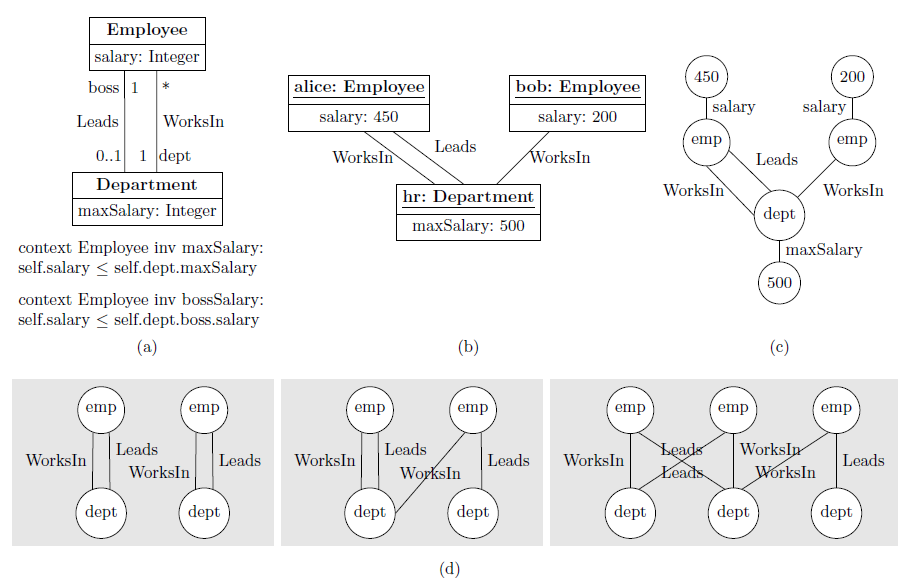
Fig 1. Motivating example: (a) UML/OCL class diagram; (b) Sample instance; (c) Encoding of the instance as a labeled graph; (d) Graph shapes of the three clusters.
We have used the USE Model Validator to generate 25 valid instances for this model. By manually inspecting these instances, we can easily realize that most of them are very similar. A designer would be interested in a smaller and more diverse set of instances that gives the same or even more information as the 25 original ones. We explain next how this can be achieved with our method.
Applying our method, each object diagram is abstracted as a labeled graph. As an example, Figure 1(c) shows the abstraction for the object diagram in Figure 1(b). We then apply hierarchical clustering to our 25 graphs using the similarity information provided by a graph kernel algorithm. From the results, validity indices recommend choosing 3 clusters. Thus, we have discovered that out of the 25 instances, there are only 3 types of solutions worth considering. The common pattern in each cluster is depicted in Figure 1(d).
Notice that one cluster identified by our method (the middle one) highlights a potential problem in the model: a department where the director works in another department. This is a corner case worth studying, to decide whether it should actually be allowed or it is a mistake in the model that needs to be fixed.
Please refer to the full paper for the full details of each phase.
Robert Clarisó is an associate professor at the Open University of Catalonia (UOC). His research interests consist in the use of formal methods in software engineering and the development of tools and environments for e-learning.




Recent Comments