Efficient Model Partitioning for Distributed Model Transformations

In our previous post, we presented ATL-MR, a distributed engine for Model Transformations (MTs) with ATL on MapReduce. The present blog extends this work and introduces our solution for efficient model partitioning for distributed MTs, recently accepted @SLE16. This work is the fruit of a collaboration with the miso team.

We propose a data distribution algorithm for declarative model transformation based on static analysis of relational transformation rules. The process starts by extracting knowledge about data access patterns based on the transformation footprints. Driven by the extracted footprints, and based on recent results on balanced partitioning of streaming graphs, we propose a fast data distribution algorithm. We validate our solution by applying it to ATL-MR, a distributed MT engine for the ATL on MapReduce. Hereafter, we give a teaser of our approach. For an elaborate description, please check our paper and /or check our presentation slides (at the very end of the post).

What makes model partitioning for MTs different than for other applications?

Typical application scenarios in MDE are characterized by big amounts of data, that may be represented by very large models (i.e. models with millions of elements). Against models of such size, current execution engines for MT languages easily hit the limit of the resources (IO/CPU) of the underlying machine. The wide availability of distributed clusters on the Cloud makes distributed computation an accessible solution for transforming large models. A typical data-parallel approach for distributing a model transformation across a cluster involves splitting the input model into chunks and assigning them to different machines, following a data-distribution scheme. Each machine is then responsible for transforming a part (i.e. split) of the input model. Existing distributed programming models such as MapReduce and Pregel can be used to simplify this operation.

 However, the characteristics of MT make efficient parallelization challenging. For instance, typical MapReduce applications work on flat data structures (e.g. logs) where input entries can be processed independently and with a similar cost. Hence, a simple data distribution scheme can perform efficiently. Conversely, models are usually densely interconnected, and MTs may contain rules with very different complexity. Moreover, most of the computational complexity of MT rules lies in the pattern matching step, i.e. the exploration of the graph structure. Because of this, model transformations witness higher ratio of data access to computation w.r.t. typical scientific computing applications. With a naive data-distribution scheme, the execution time can be monopolized by the wait time for model elements lookup. With an unbalanced distribution, machines with light workload have to wait for other machines to complete. At other times, machines with heavy workload can crash when hitting their memory limit. Such challenges are not only limited to model transformations but extend to several distributed graph processing tasks.

Model partitioning by a simple example!

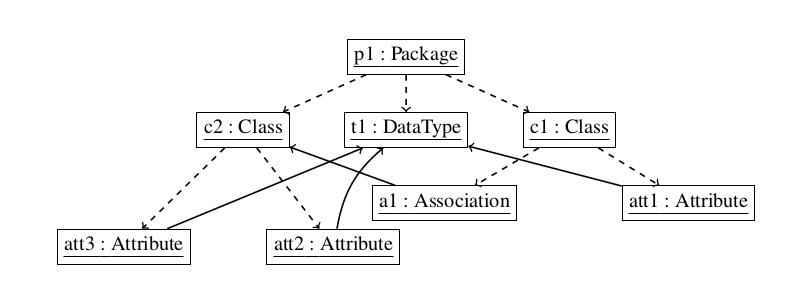
We refer to the Class2Relational transformations to motivate the need for efficient model partitioning solutions. Figure 1  depicts a simple Class diagram. We refer to containment references using the dashed arrows, and type references by continuous arrows. The model is composed of a package (p1) containing two classes (c1 and c2). Table 1 lists, for each source element, the set of elements that the ATL engine will need to read in order to perform its transformation (Dependencies). We denote by d (j) the set of dependencies of j, as referred by the column Dependencies in Table 1. For instance, d (a1) = {a1, c2}.

 Considering a system S of 2 machines (m1 and m2) computing in parallel a model transformation. A set of input model elements is assigned to each machine. We argue that a random assignment strategy could result in unfavorable performance. Nonetheless, using an adequate data distribution strategy to the cluster nodes, it is possible to optimize the number of loaded elements, and hence, improve the performance of the model transformation execution.

We consider a random uniform distribution scenario of our sample model over S. We can assume that this model is stored in a distributed persistence backend, permitting the loading of model elements on-demand. We randomly assign elements {p1,att1,c2,t1} to m1, and the remaining to m2. The splits assigned to m1 and m2 are denoted by A1 and A2 respectively. We identify the weight of a split assigned to a machine i (Wi), as the number of elements to be loaded in order to perform its transformation. Assuming that every machine has a caching mechanism that keeps elements that have already been looked up in memory, loading model elements is considered only once.

 Therefore, W(A1) is the cardinality of the set resulting from the union of the dependencies of all the elements assigned to the machine i ( |⋃(e ∈ Ai) d(e) | ), that is,  |{p1, c1, a1, att1, c2, att2, att3 ,t1}| = 8. Likewise, W(A2) = |{c1, a1, att1, c2, att2, att3, t1}| = 7. As noticed, both machines need almost all the model to perform the transformation of the split assigned to them, resulting in an overall remote access to the underlying persistence backend of 15 (=8+7) elements. However, this naive distribution scenario leads to the worst overall remote access. As the elements {p1,c1,a1,att1} share a heavy dependency between each other, it makes more sense to assign them to the same machine (e.g. m1). The rest are hence assigned to m2. This scenario results in better weights. Precisely, W(A1)  = 6 and W(A2) = 4, with an overall remote access of 10 (6+4).

Computing such efficient split becomes especially challenging when we consider model graphs with millions of nodes. Without a fast heuristic, the cost of traversing these large graphs to compute the splits may overcome any possible benefit of data distribution.

How we efficiently distribute our input model?

 We rely on static analysis of the transformation language to compute an approximated dependency graph. The building process of this graph relies on transformation footprints.

These footprints represent an abstract view of the navigation performed by a given rule application. Footprints are a simplification of the actual computation, and they originate a dependency graph that is a super-graph approximation of the actual one. We will then apply greedy data-distribution algorithms from recent related work to the approximated dependency graph.

The execution overview of our proposed solution is depicted in Figure 2. The framework starts by passing the transformation to the static analyzer in the master node for footprints extraction. Footprints are fed to the splitting algorithm to assist its assignment decision making. As the model stream arrives, the master decides to which split a model element should be assigned. Once the stream is over, the slave nodes proceed with the transformation execution.

 If you’re interested in our algorithms as well as our system formalization,  you can check our paper!

Extending ATL-MR with efficient model partition

 Our solution is implemented as a feature of our distributed engine ATL-MR, which it is a prototype distributed engine for running complex ATL transformations on top of MapReduce. ATL-MR is implemented as an extension of an existing ATL VM and runs in two steps, Local-MatchApply (map), and GlobalResolve (reduce). Each mapper is assigned a subset of model elements using a splitting process. For each model element, if it matches the input pattern of an existing rule, then a target element is created together with tracing information, and target properties corresponding to elements locally assigned are resolved. Information about non-local elements is stored in traces and sent to the reduce phase for a global resolve. This step is responsible for composing the sub-models resulting from the previous phase into a single global output model. More elaborate description of the algorithm can be found at this link.

 ATL-MR is coupled with a decentralized persistence backend, NEOEMF/COLUMN, built on top of HBase and ZooKeeper. It offers a lightweight on-demand loading and efficient garbage collection and model changes are automatically reflected in the underlying storage, making changes visible to all the clients. It also supports pluggable caching mechanisms.

 In order to perform an automated footprint extraction operation, we rely on a static analysis tool of ATL transformations, anATLyzer. Although it was initially implemented to automate errors detection and verification in ATL transformations, in our solution, we use anATLyzer internals, especially, typing information inference of OCL expressions, in order to construct the footprints of ATL rules.

 The greedy algorithm is implemented on top of a Hadoop TableInputFormat class. This class is the one responsible for partitioning HBase tables. We override its default behavior and enable the use of our custom splitting solution. The implementation relies on the HBase storage scheme, where, <key, value> pairs are grouped by family and stored in increasing lexicographical order. Table splits are defined by a start key and end key. In our solution, we associate to each split an ID. Later on, we use this id to salt the row keys belonging to the same splits. We applied our splitting approach to the LocalResolve phase of ATL-MR algorithm. The Global resolve uses a random assignment approach.

How we perform!

 We evaluate the performance of our proposed solution while running it on a well-known model transformation, Class2Relational. We use as input randomly generated models with diverse sizes (we provide generation seeds to make the generation reproducible). The generator is highly configurable. The default configuration takes as input the model size, the density of references, and the variation. The variation applies to both the model size, and the number of references to be generated per property. In our experiment, we used a density of 8, and a variation of 10%.

 The Hadoop framework comes with tools to help to analyze data being processed. This feature gathers statistics about the job, for different purposes like quality control or application level statistics. Each counter is maintained by a mapper or reducer and periodically sent to the application master so it can be globally aggregated. Counter values are definitive only once a job is successfully completed. Hadoop allows user code to define user-defined counters, which are then incremented as desired in the mapper or reducer. We defined a Hadoop counter for globally reporting metrics about data access and update. This counter was integrated with our distributed persistence backend, NEOEMF/COLUMN . It globally reports remote access count, local access count at the end of every successful job. We believe that such metrics are relevant as they can be decoupled of the internal complexities of both the transformation and persistence engines. or each model size, we generate three random models. For each model size, we generate three random models. Each execution of the transformation on the generated model is launched with a fixed number of nodes (2..8).

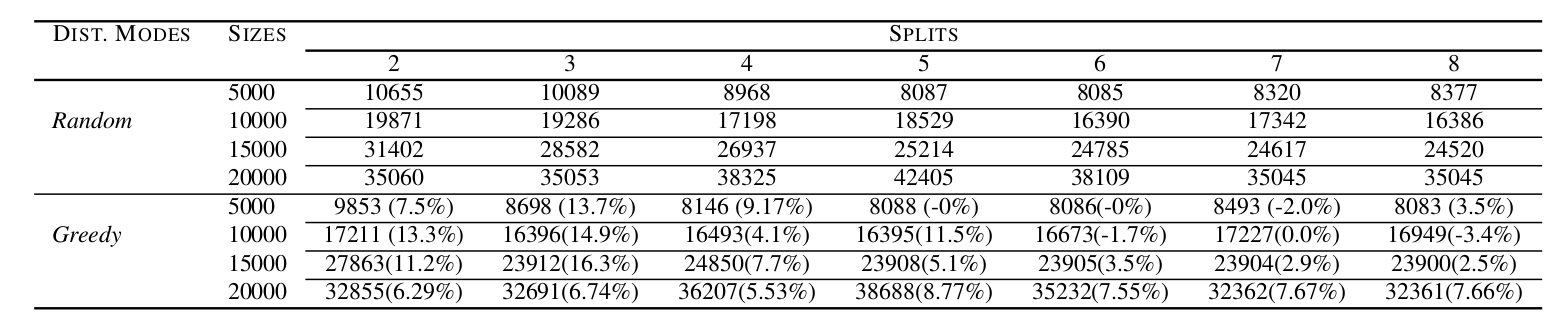
 The average improvement results expressed in term of the number of accesses to the underlying backend is summarized in Table 2. Each access either fetches an element or its properties. Our distributed solution shows an average improvement up to 16.7%. However, in some cases, the random distribution performed better than our greedy algorithm, mostly for the set of models with sizes 5000 and 10000. For the smallest set of models, it did not bring any improvement, on average, with 5 and 6 splits respectively.

 Table 2: Remote access count (per properties): Random Vs. Greedy

What comes next?

In our future work we intend to improve the efficiency of our distributed transformation engine by exploring the following lines:

• Extending our work to balanced edge partitioning and conducting a thorough study on the impact of the model density on the partitioning strategy.

• Improving the distribution of, not only the input model of the transformation but also its intermediate transformation data (tracing information)

• Applying our approach to distributed model persistence for any model transformation-based application. We plan to design a model-persistence framework that would decide, at model-element creation time, which machine should host the element, by exploiting knowledge about its possible future transformations.