This post discusses the representation of Belief Uncertainty in software models. This kind of uncertainty refers to the situation in which the modeler, or any other belief agent, is uncertain about the behavior of the system, or the statements that the model expresses about it. In this work, we propose to assign a degree of belief to model statements (let they be constraints or any other model expression), which is expressed by a probability (called credence, in statistical terms) that represents a quantification of such a subjective degree of belief. We discuss how it can be represented using current modeling notations, and how to operate with it in order to make informed decisions. This work has been accepted at the 11th Workshop on Modelling in Software Engineering (MiSE’2019).
Contents
Uncertainty in Software Modeling
The explicit expression of Uncertainty in software models is gaining recognition as an effective means to faithfully represent and operate with the unknowns and imprecise information which are inherent to any system that works in a physical environment [1] or that integrates Artificial Intelligence (AI) components. Due to the “black-box” nature of AI, modeling and analyzing such systems typically requires accepting some uncertainties about their precise behavior.
In general, uncertainty applies to physical measurements, estimations, predictions of future events, or unknown properties of a system. It can be defined as “the quality or state that involves imperfect and/or unknown information” [2].
Despite this apparently clear definition, the term uncertainty still remains imprecise, since it embodies different kinds of uncertainties, each one requiring a different representation, and exhibiting different characteristics. For instance, measurement uncertainty (MU) refers to the inability to know with complete precision the value of a quantity [2], [3], and it is normally expressed by means of a number that represents the possible deviations of the values of the measured quantity; e.g., x = 3.0 ± 0.01. Another example is occurrence uncertainty (OU), which refers to the likelihood that a physical entity represented in a model actually occurs in reality; it can be expressed by means of a real number in the range [0..1] that represents the probability assigned to such an occurrence [4]. In order to describe and classify these types of uncertainty and others like content, occurrence, time, environment, geographical location, belief and indeterminacy uncertainty [5], a conceptual model called U-Model has been proposed [1], and there is an OMG effort to define a metamodel for Uncertainty Modeling [6].
In this paper, we are interested in Belief Uncertainty (BU), which refers to the situation where a belief agent is uncertain about a statement made about the system. In this case, a belief statement is normally subjective, and refers to current or future states or properties of the system being modeled, or its environment. For example, we can not be fully sure whether the sensor providing the value of an attribute is operating correctly, or whether the precision of the sensor is correct.
Furthermore, belief statements can also refer to the way in which we have modeled the system. For example, a stakeholder cannot be fully sure whether the formula employed to compute a derived value in a system is correct, since we may not have a complete understanding on how the system works.
This paper aims at answering the following questions:
- How can we explicitly specify the belief uncertainty that a belief agent has about a system or about its model?
- How can we incorporate such information in the models, using existing modeling notations?
- Once specified and represented, how can we operate with belief uncertainty in order to be able to make informed decisions, and to reason about the system behavior?
To represent belief uncertainty, we will use the degree of belief that a belief agent assigns to a model statement [7]. In general, such a degree of belief can be measured using qualitative or quantitative methods, such as a grade or a probability. In this work, we will use Bayesian probabilities, which is the classical model for quantifying subjective beliefs [8], and more precisely the concept of credence. Credence is a statistical term that refers to a measure of belief strength, which expresses how much an agent believes that a proposition is true [9]. For example, a modeler can be 99% sure about the behavior of the rule that decides whether an alarm should be fired or not, or that the type used to represent a given entity is correct.
Representing and operating with Belief Uncertainty in software models is relevant in several situations, like for example:
- When dealing with a physical system whose behavior is not fully
- When our knowledge about the system is not
- When the model admits different interpretations, depend- ing on the belief agent interacting with the system. For instance, the credibility assigned by two different people to the system functionality that decides if a room is hot or cold may be different depending on subjective feelings of each
- When a model is automatically inferred by a machine (either by performing model mining activities on soft- ware/data repositories [10] or by Artificial Intelligence techniques [11]) which may not be complete, accurate or consistent. Our decisions about the way in which we have modeled the system need to be qualified with some degree of
In all these cases, the models may not be truthful enough, and it is important to count on mechanisms that enable us to assess such uncertainty and to measure somehow the possible deviations between the actual system and the model that represents it [12], as well as the differences between individual interpretations or judgments made by separate belief agents about the system.
This paper can be considered as an extension of our previous work [4], where we used probabilities to represent the degree of belief (we called it confidence) that the modeler assigns to the actual occurrence of an entity, given that it appears as an object or a link in a model (UML class diagrams in our specific examples). Thus, model elements can be enriched with information that could assess their truthfulness. In [4], beliefs were based on objective evidences. This paper extends that work in three different dimensions. First, beliefs are not limited to objects and links, but they can be applied to any model element. Second, beliefs do not apply only to the occurrence of these objects or links, but to any property or state of the system, or of its individual elements. Third, contrarily to the objective nature of occurrence uncertainty, belief uncertainty can be completely subjective. It can also be differently specified by individual belief agents. Our work is also aligned with the U-Model [1] proposal and the OMG PSUM RFP [6], providing a materialization of their concepts, and hence trying to serve as a proof of concept for them.
Background on Uncertainty
Belief uncertainty
Uncertainty can be defined as the quality or state that involves imperfect and/or unknown information. It applies to predictions of future events, estimations, physical measurements, or unknown properties of a system [2]. We can distinguish between aleatory and epistemic uncertainty [12]. Aleatory uncertainty refers to the inherent variation associated with the physical system under consideration, or its environment. In contrast, epistemic uncertainty refers to the potential inaccuracy in any phase of the modeling process that is due to the lack of knowledge.
In this paper, we are interested in Belief Uncertainty (BU), which is a particular kind of epistemic uncertainty that refers to the situation where a belief agent is uncertain about a statement made about something, in this case a system and its environment.
To express such an uncertainty, the belief agent assigns to a statement a degree of belief, which can be represented using qualitative or quantitative methods, i.e., a grade or a probability. In this paper, we will consider probabilities.
A statement qualified by a degree of belief is called a belief statement. Examples of belief statements in our context are: “Bob is 90% sure about the validity of the temperature readings made by the sensor” (because he is not sure if the sensor is working properly all the time), “Mary is only 20% confident of the result returned by the method m()” (because she is not sure of the formula used by the method to compute it), or “the modeler has a confidence of 95% that the value assigned to variable X is the correct one” (since it has been derived from data which is not fully reliable).
Belief statements are always made by a belief agent, a physical entity that holds one or more beliefs. It could be a human individual or a group, an institution, or even a machine. In general, any stakeholder of the system that expresses some belief about it. It is essential to note here that a belief agent should be capable of deriving judgments or of conducting actions based on its beliefs [1], and hence the importance of being able to reason about the belief statements and the degree of belief assigned to them. Of course, different belief agents may assign different degrees of belief to the same statement, depending on their judgments, subjective reasons or particular evidences.
Credence and Bayesian probabilities
Credence is a statistical term that refers to a measure of belief strength, which expresses how much an agent believes that a proposition is true [9]. It is normally expressed as a percentage or a number in the range [0..1], and can be defined and understood in the context of the subjective interpretation of Probability [15], whereby a probability (a credence) represents a quantification of a personal belief [8]. Bayesian probability is the most classical model for expressing and operating with subjective information, and hence for quantifying beliefs. Credence values can be based entirely on subjective feelings.
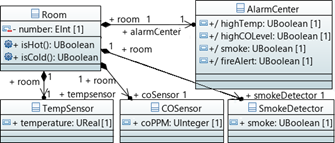
Fig. 1. A smart hotel with monitorizable rooms.
Moreover, credence is better understood in the context of gambling, where this concept is directly related to the odds at which a rational person would place a bet.
Uncertain OCL/UML datatypes
In [16], we extended the OCL/UML [13], [14] datatypes to incorporate information about the uncertainty of their values. In particular, we applied subtyping to extend the types UnlimitedNatural, Integer, Real, and Boolean and we defined the new datatypes UUnlimitedNatural, UInteger, UReal and UBoolean.
To capture the uncertainty of numeric values, they are represented by pairs of numbers: (x, u) with x the expected value and u the associated standard uncertainty [2]. For instance, we can represent the height of a person that is 170 ±0.5 cm with the uncertain integer value UInteger(170, 0.5). In UBoolean values, the uncertainty does not refer to measurement uncertainty, but to confidence. Thus, a UBoolean value is a pair (b, c) where b is a boolean value (true, f alse) and c is a real number in the range [0..1], representing the confidence that b is certain.
Expressing Belief Statements in Models
Motivating example
A hotel has rooms equipped with sensors that monitor their temperature, level of CO (measured in parts per million, PPM), and the presence of smoke. Devices (whose type is AlarmCenter) are installed in the rooms, too. They provide four indicators, one for each possible alarm that can be detected: high temperature, high CO level, smoke, and fire alert. Fig. 1 shows the system modeled in the UML tool Papyrus [17]. The values of the attributes of the AlarmCenter can be derived from the values of the sensors, using the following derivation rules:
context AlarmCenter
highTemp : UBoolean derive:
self.room.tempSensor.temperature > 30.0
highCOLevel : UBoolean derive:
self.room.coSensor.coPPM > 20
smoke : UBoolean derive :
self.room.smokeDetector.smoke
fireAlert : UBoolean derive:
highTemp and highCOLevel and smoke
Additionally, rooms provide two query operations, to check whether it is hot or cold inside:
context Room isHot() :UBoolean = self.tempSensor.temperature>25 isCold():UBoolean = self.tempSensor.temperature<18
The measurement uncertainty associated to the sensed val- ues needs to be propagated through the operations. This is why the derived attributes of class AlarmCenter and the operations of class Room are of type UBoolean.
Further constraints are used to set bounds in some model parameters. For example, the following invariant sets an upper limit on the precision of the temperature sensors, e.g., based on the information provided by the device technical manuals.
context TempSensor inv TempPrecision: self.temperature.uncertainty() <= 0.2
The invariant uses the uncertainty() operation defined for UReal numbers, which returns their precision [16].
Belief statements by example
In addition to the measurement uncertainties already specified in the model, the following are examples of belief statements that represent the possible beliefs of two belief agents, Bob and Mary, about the system:
- We know that CO and smoke sensors have a reliability of 90%; e., 10% of their readings are not meaningful.
- We can only be 98% sure that the precision stated in the manuals of TempSensor devices is 0.2 Such a degree of belief goes down to 90% for the CO and smoke sensors, since they are cheaper.
- Both agents are only 95% confident that the presence of high temperature, high level of CO and smoke means that there is a fire; in other words, they have a 95% degree of belief in the expression that derives the value of attribute fireAlert of class AlarmCenter.
- Bob does not trust the expressions used in the queries isCold() and isHot(), because he is from the south: when the room says it is hot, in fact, he thinks the temperature is fine; similarly, sometimes he feels cold but the room says it is not. So he assigns just a 50% credibility to these expressions. Mary, however, thinks that these expressions are 99% accurate because they both reflect rather well how she always feels in the
- Despite apparently connected, the cheap CO and smoke sensors may be broken or with no battery, and hence it is similar to not having them connected. So, they think the chances that they are not working are 5%.
- Since room number 3 is adjacent to the hotel kitchen, temperature alerts are frequent in that room. This is why everyone pays little attention to them, estimating that 90% of the alerts are false
- Bob doubts whether the type of attribute number of class Room is Integer or not, since he thinks its values could also contain characters different from
- Similarly, they also express their doubts about other modeling elements and constraints such as the multiplicity of some association ends: should a sensor always be attached to exactly one room? Could it be attached to none, or to several?
Expressing Degrees of Belief
Although apparently similar, the previous belief statements express various kinds of beliefs, in different ways.
- The first one is about the validity of the value of an attribute (temperature, coPPM or smoke). This is dif- ferent from the precision of the value, which is already expressed by means of the extended uncertain datatypes. Expressing the degree of belief about the validity of an attribute or return value of an operation can be realized by assigning a credence to that attribute, or return
- Statement number (2) is about the degree of belief that the belief agents assign to a statement in the model; in this case, to the OCL constraint TempPrecision.
- The third case corresponds to assigning a credence to an OCL expression, in this case the one to derive the value of attribute fireAlert.
- The fourth statement is similar to the previous one, the only difference being that each agent assigns a different credence to the expressions in the query
- Belief statement (5) can be expressed in two First, by assigning a credence to the multiplicity in the associations between the room and the sensors that forces that there should always be a sensor of each kind connected to a room. Second, we could assign a credence to the associations to represent the confidence we have on their occurrence, as described in [4].
- The previous belief statements were made in general for all instances of a type (sensor, room, operation). Belief statement (6) shows an example of a situation in which the degree of belief of a statement is made about one particular instance (the value of attribute HighTemp of room r3), by all belief
- The last two belief statements refer to the model itself, and how their elements have been used to represent the physical system. In particular, the first one is unsure about the type used for a variable, and the second one about a multiplicity. Thus, the two examples mentioned above can be expressed by assigning degrees of belief to the corresponding OCL constraints:
context Room inv:
self.number.oclIsTypeOf(Integer)
context AlarmCenter inv:
self.room->size() = 1
In summary, we need to assign probabilities to the different kinds of model elements present in UML class diagrams and its OCL constraints:
- Classes and Associations. In this case, the probability represents the degree of belief that an agent assigns to the actual occurrence of an entity or a relationship, given that it appeared as an object or a link in the model. This is fully consistent with our proposal in [4].
- Probabilities associated to attributes represent the degree of belief assigned to the validity of that attribute. Note how this semantics is consistent with the one given to associations when regarding the attribute as a bidirectional association between the class and the attribute’s datatype.
- Operations also need to be considered, and it should be possible to assign degrees of beliefs to their return
- Probabilities assigned to OCL expressions and invariants indicate the degree of belief we assign to them.
Note that, by convention, if no agent is explicitly stated, we assume the degree of belief is shared by all of them. Similarly, if a belief statement is made for particular types of objects (e.g., sensors or rooms), we assume it applies to all instances of those types.
Belief Statements in UML models
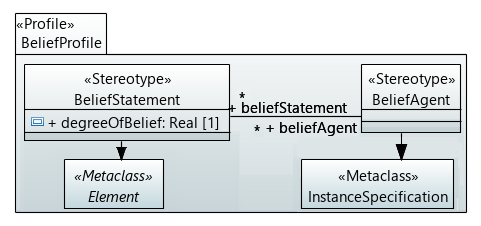
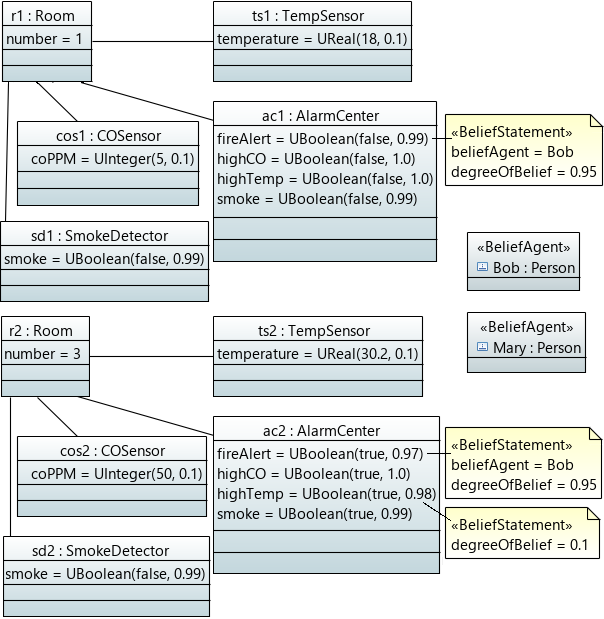
To apply these concepts to software models, we need to appropriately map them to the corresponding concepts used in modeling notations. The most obvious manner to add information to a UML model is by applying a UML Profile, which permits enrich- ing the model elements with extra information or additional semantics. In this case, the information that we want to add is the degree of belief assigned to model elements (by means of a credence) and the belief agent who is making the belief statement. This is represented in the Belief UML profile we have developed in Papyrus and show in Fig. 2. Fig. 3 shows an example of an object model that applies the profile. It corresponds to the hotel rooms described earlier in this section. Additional OCL queries (with the proper credence assigned to them) could then be used to express beliefs on particular instances of the types.
The UML profile mechanism is expressive enough (at least, based on the initial experiments that we have conducted) to represent the kinds of belief statements that we have identified in that example. It is also the way suggested to incorporate uncertainty in UML models by other authors, e.g., [1], [5]. Nevertheless, it does not provide an easy way to operate with the degrees of belief themselves, not to mention their propagation. The next section covers how we have translated and formalized the Papyrus UML models annotated with our profile with the USE tool [18] and its SOIL language [19].
Calculating Degrees of Belief
The USE tool [18] provides an environment for the specification and execution of systems enriched with behavior using a high-level behavioral language called SOIL [19]. Operation bodies (defined in begin…end blocks) can be specified with SOIL constructs for the creation and deletion of objects and links, variable assignment, loops, etc. USE specifications enriched with SOIL can therefore be executed.
The strategy to explicitly assign belief degrees to the model elements and OCL expressions will depend on the kind of element, although, in general, we will use a common pattern (in fact, this part of the USE specification could be automatically derived from any input UML model annotated with the UML profile described above). For each element X we will define two new elements:
- A set X_Beliefs of pairs (a, b) where a is a belief agent and b ∈ [0..1] is the degree of belief that agent a assigns to that
- A query operation X_credence(a:BeliefAgent):Real that returns the degree of belief that the agent a has assigned to that element. In case no agent has assigned a degree of belief, it returns the value by default, which is 1.
To specify a degree of belief for all agents, we will simply use the OCL special value null as belief agent.
Let us illustrate this process in the case of the isHot() query operation. First, we define for it the corresponding set of pairs that will store the agents’ credences:
isHot_Beliefs : Set(Tuple(beliefAgent :BeliefAgent,
degreeOfBelief:Real))
This structure has an associated operation for adding pairs to the set (to avoid duplicated assignments, it removes previous beliefs by the same agent, if any, before adding the new one):
isHot_BeliefsAdd(ba:BeliefAgent,d:Real)
begin
self.isHot_Beliefs := self.isHot_Beliefs->
reject(t|t.beliefAgent=ba)->
including(Tuple{beliefAgent:ba,degreeOfBelief:d})
end
With this, the query operation that calculates the corresponding credence assigned by each belief agent is as follows
isHot_credence(a:BeliefAgent): Real =
let baBoD : Set(Tuple(beliefAgent:BeliefAgent,
degreeOfBelief:Real)) =
self.isHot_Beliefs->select(t|t.beliefAgent=a) in
if baBoD->isEmpty then 1.0
else baBoD->collect(degreeOfBelief)->any(true)
endif
If we have a system where r1 is a room, we can create two belief agents, Bob and Mary, and specify their degrees of belief on the operation isHot() of room r1, as well as a default degree of belief of .95 for all agents different from Bob and Mary as follows:
Hotel> !new BeliefAgent('Bob')
Hotel> !new BeliefAgent('Mary')
Hotel> !r1.isHot_BeliefsAdd(Bob,0.5)
Hotel> !r1.isHot_BeliefsAdd(Mary,0.99)
Hotel> !r1.isHot_BeliefsAdd(null,0.95)
Note that the value by default, would be 1.0 if not specified. If, now, assuming that the temperature of room r1 is 25.3, we query the model with USE, we obtain:
Hotel> ?r1.isHot() -> UBoolean(true,1.0) : UBoolean Hotel> ?r1.isHot_credence(Bob) -> 0.5 : Real Hotel> ?r1.isHot_credence(Mary) -> 0.99 : Real Hotel> ?r1.isHot_credence(null) -> 0.95 : Real
Another operation, isHot_BeliefsRm(ba:BeliefAgent), can be used to delete degrees of belief assigned by an individual agent (the default value is adopted then). Finally, we can also use the initialization value to set a default value for all agents:
isHot_Beliefs : Set(Tuple(beliefAgent : BeliefAgent,
degreeOfBelief : Real))
init : Set{Tuple{beliefAgent : null,
degreeOfBelief : 0.85}}
The same process we have shown here for an operation can be followed to assign degrees of belief to the attributes of a class, to the class itself (a generalization of the “prob” attribute that we defined in [4]), and to OCL constraints.
The additions that we propose to incorporate belief uncer- tainty to the other kinds of model elements are as follows:
- For a class C, a new attribute with the set C_Beliefs and a new operation C_credence(a:BeliefAgent):Real will be added. They will be used to store and query about the degree of belief expressed by the corresponding agents about the occurrence of the instances of the
- For an attribute x whose type is a datatype T , the new attributes x_Beliefs and the new operation x_credence(a:BeliefAgent):Real will represent the validity assigned to the values of the attribute (independently from the values themselves).
- Similarly, in case of an attribute r whose type is a classifier C (i.e., r is a reference to an object of class C), the r_credence(a:BeliefAgent) operation will represent the degree of belief that agent a has about such a reference. This also applies to the role ends of the associations the class is engaged in. For example, role coSensor is considered as another attribute of class Room.
- Operations f ():T are treated similarly: attribute f _Beliefs and operation f _credence(a:BeliefAgent):Real represent the validity assigned to the return values of the operations, as in the case of If an operation has arguments affected by belief uncertainty, the degrees of belief of the arguments should be considered when executing the operation, since the uncertainty should be propagated.
- Invariants will be represented by the equivalent Boolean operations in the class that provides their context [20]. Thus, for every invariant “context C inv I”, a new op- eration I():Boolean will be added to class C, together with the corresponding attribute with the set I_Beliefs and operation I_credence(a:BeliefAgent):Real.
- To assign a degree of belief to the results of an OCL expression, we can convert it into an operation. How the individual degrees of belief of the operands and operations that comprise the expression are combined to produce a degree of belief of the result is discussed next.
- Expressions such as derive and init on attributes can be treated as assignment expressions, and as such, they can also have an associated degree of belief.
Propagating degrees of belief
Once we are able to express the degree of belief assigned to the individual modeling elements, this section describes how the associated credence can be propagated through the operations. This is possible because we have provided an operational specification of these assignments in the previous section.
To illustrate how propagation works, let us look at the attribute fireAlert of class AlarmCenter. First, it may have an associated credence about its validity (fireAlert_Beliefs). Second, its values are defined by a derived expression, to which agents can assign degrees of belief (fireAlertExpr_Beliefs). And third, the expression should aggregate the degrees of belief of each one of its constituent components (HighTemp_Beliefs, highCOLevel_Beliefs, and smoke_Beliefs). In this case, the aggregation function corresponds to an and operation. We could simply assume the variables are independent, and then multiply the corresponding degrees of belief.
Then, the credence of fileAlert is ‘qualified’ by the degree of belief on the expression:
fireAlert_credence(ba:BeliefAgent): Real =
let baBoD : Set(Tuple(beliefAgent:BeliefAgent,
degreeOfBelief:Real)) =
self.fireAlert_Beliefs->
select(t|t.beliefAgent = ba) in
(if baBoD->isEmpty then 1.0
else baBoD->collect(degreeOfBelief)->any(true)
endif) * self.fireAlertDeriveExpr_credence(ba)
And, in turn, the degree of belief of the expression is qualified by the aggregated credence of the operands:
fireAlertDeriveExpr_credence(ba:BeliefAgent): Real =
let baBoD : Set(Tuple(beliefAgent:BeliefAgent,
degreeOfBelief:Real)) =
self.fireAlertDeriveExpr_Beliefs->
select(t|t.beliefAgent = ba) in
(if baBoD->isEmpty then 1.0
else baBoD->collect(degreeOfBelief)->any(true)
endif)
* highTemp_credence(ba)
* highCOLevel_credence(ba)
* smoke_credence(ba)
The system can be simulated now with USE, and the behavior of the operations checked. For example, the following listing shows how the room is created, their sensors and alarm center added, and agent Bob sets his degrees of belief.
Hotel> !new Room('r1')
Hotel> !r1.number := 1
Hotel> !new COSensor('co1')
Hotel> !new TempSensor('ts1')
Hotel> !new SmokeDetector('sd1')
Hotel> !new AlarmCenter('ac1')
Hotel> !insert (r1,ts1) into Temp
Hotel> !insert (r1,co1) into CO
Hotel> !insert (r1,sd1) into Smoke
Hotel> !insert (r1,ac1) into RoomAlarmed
Hotel> !ts1.temperature := UReal(31.0,0.1)
Hotel> !co1.coPPM := UInteger(50,0.1)
Hotel> !sd1.smoke := UBoolean(true,0.99)
Hotel> !new BeliefAgent('Bob')
Hotel> !new BeliefAgent('Mary')
Hotel> !r1.isHot_BeliefsAdd(Bob,0.5)
Hotel> !r1.isCold_BeliefsAdd(Bob,0.5)
Hotel> !r1.correctRoomNumberType_BeliefsAdd(Bob,0.8)
Hotel> !r1.alarmCenter.fireAlert_BeliefsAdd(Bob,0.99)
Hotel> !r1.alarmCenter.fireAlertDeriveExpr_BeliefsAdd(Bob,0.95)
Hotel> !r1.alarmCenter.highTemp_BeliefsAdd(Bob,0.99)
Hotel> !r1.alarmCenter.highCOLevel_BeliefsAdd(Bob,0.99)
Hotel> !r1.alarmCenter.smoke_BeliefsAdd(Bob,0.99)
Now, we can easily check the resulting confidence that each agent has on the current value of the fireAlert attribute as follows:
Hotel> ?r1.alarmCenter.fireAlert -> UBoolean(true,0.99) : UBoolean Hotel> ?r1.alarmCenter.fireAlert_credence(Bob) -> 0.9125662095 : Real Hotel> ?r1.alarmCenter.fireAlert_credence(Mary) -> 1.0 : Real Hotel> ?r1.alarmCenter.fireAlert_credence(null) -> 1.0 : Real
After taking into consideration all the different degrees of belief that Bob has assigned to all elements and expressions, the confidence that he has on the fire alert of room r1 is reduced to 0.91. Interestingly, given that the high temperature alert of room 3 had a confidence of 0.1 (since it was close to the kitchen), based on Bob’s confidence on the rest of the model elements, his credence on the fire alarm is only 0.09. The UML profile as well as the Papyrus and USE/SOIL files for our example are available for download from our Git repository.
Related Work
In [5] the authors propose a conceptual model, called Un- certum, which is supported by a UML profile (UUP, the UML Uncertainty Profile) that enables the inclusion of uncertainty in test models. Uncertum is based on the U-Model [1] and extends it for testing purposes. UUP is a very complete profile that covers all different kinds of uncertainties. UUP was de- fined mainly for test modeling, i.e., creating test-ready models that can be used to generate executable test cases. Therefore such type of modeling is merely descriptive, i.e., mainly for annotation purposes. This is why most of the information it captures is in textual form, i.e., using Strings. Instead, we are interested in both representing belief statements and operating with them, and therefore we need to be more precise.
Representing and reasoning about degrees of belief can be done using different theories. In this initial work, we have proposed the use of Probability theory [8], [21]. Other authors have proposed other approaches including Possibility theory (based on fuzzy logic [22], [23]), Plausibility (a measure in the Dempster-Shafer theory of evidence [24]) or Uncertainty theory [25]. The comparison among these theories falls out of the scope of this paper, although an interesting discussion can be found in [25]. Our decision was based on simplicity: probability theory is well-known and understood by most domain experts, who could more easily use it to represent confidence in their model elements—particularly when the betting analogy is used to determine the values of the degrees of belief. In contrast, the complexity of the other approaches could hinder their correct application and, therefore, risk their potential benefits.
As mentioned in the introduction, this work can be con- sidered as a generalization of our proposal for modeling occurrence uncertainty of objects and links in a model [4] using probabilities. In this work, we used the notion of confidence—which is commonly used in the literature, for example, Denney et al. [26] used it to describe and reason about the credibility of safety claims. Here, we have extended confidence to general beliefs, which can be subjective and separately assigned by individual agents, and refer to any statement about the system being modeled, and not only to objects and links. Thus, instead of confidence, we use the term credence, which is more precise and technically more appropriate to represent subjective degrees of belief.
The OMG is working towards a metamodel for the precise specification of uncertainty (PSUM) [6]. Our work is aligned with the terms defined in the RFP, and aims at providing some examples that could be used to validate the proposals.
There are other modeling works that deal with uncertainty in models, but they usually focus on aspects of uncertainty different from the ones we have described here. For instance, some works focus on the uncertainty on the models themselves and on the decision of right type of models to use depending on the system properties that we want to capture [27]. Other works deal with the uncertainty of the design decisions, of the modeling process, or of the domain being modeled [28]–[31].
Our work does not deal with the possible modeling choices; we just treat a model as a set of statements [7] and permit assigning degrees of belief to them. Nevertheless, we believe there is some overlap between the two notions of uncertainty that we will explore as part of our further work.
Conclusions and Future Work
This contribution proposes the explicit representation and management of the information about the degree of belief that an agent has on the statements expressed in a model about the system it represents. We have discussed how such degrees of belief can be represented, and illustrated our proposal with one exemplar case study.
The initial ideas presented in this paper can be extended and continued in various directions. First, we are now able to assign degrees of belief to model elements, statements and expressions, but we would like to assign belief to patterns, paths in a model, etc. We would also like to make beliefs first class concepts and be able to assign belief degrees to other agents’ beliefs.
Moreover, we currently assign degrees of belief to modeling elements regardless of their value, an assumption which may not hold in a realistic setting. For instance, in our hotel example, an agent may believe that false positives are more likely than false negatives. Thus, we will explore how to define degrees of belief for the possible values of an element, e.g., using continuous or discrete functions. Associating evidences to belief statements would be interesting too, in addition to credence and belief agents.
We also plan to represent and operate with degrees of belief in other modeling elements not contemplated here, such as use cases, state machines, pre and post conditions, activities, etc. Bayesian probabilities is the most classical model for quantifying beliefs. However, when it comes to reasoning with beliefs under partial knowledge, Bayesian probabilities have shown some limitations. To cope with these issues, the Transferable Belief Model (TBM) [32] addresses the same concepts, except it does not rely on probabilistic quantification, but on a more general system based on belief functions. We would like to investigate the use of the TBM on top of the
Bayesian model for representing degrees of belief. However, when it comes to reasoning with beliefs under partial knowledge, Bayesian probabilities have shown some limitations. To cope with these issues, the Transferable Belief Model (TBM) [32] addresses the same concepts, except it does not rely on probabilistic quantification, but on a more general system based on belief functions. We would like to investigate the use of the TBM on top of the
More and larger case studies should give us more feedback on the features and expressiveness of our approach. Moreover, validation with industrial modelers and users would help us validate its applicability, usability and effectiveness.
We are also working on the integrated support of all these mechanisms within modeling tools. So far, we have used Papyrus to create the UML models annotated with our profile and USE/SOIL for the execution and propagation of belief. We plan to (1) explore how to automatically generate the USE specifications from the Papyrus UML models, and (2) how the execution and propagation of belief could be fully integrated in Papyrus using fUML and Moka.
Finally, we also intend to use this work in the context of the Modelia initiative. When the development of software relies on Machine Learning or Artificial Intelligence components, there is always some degree of confidence, precision or uncertainty on the results. We will need to be able to represent it and operate with it in our models.
References
[1]M. Zhang, B. Selic, S. Ali, T. Yue, O. Okariz, and R. Norgren, “Understanding uncertainty in cyber-physical systems: A conceptual model,” in ECMFA’16, ser. LNCS, vol. 9764. Springer, 2016, pp. 247–264.
[2]JCGM 100:2008, Evaluation of measurement data—Guide to the expres- sion of uncertainty in measurement (GUM), Joint Com. for Guides in Metrology, 2008, http://www.bipm.org/utils/common/documents/jcgm/pdf.
[3]JCGM 200:2012, International Vocabulary of Metrology – Basic and general concepts and associated terms (VIM), 3rd edition, Joint Commit- tee for Guides in Metrology, 2012, http://www.bipm.org/utils/common/ documents/jcgm/JCGM_200_2012.pdf.
[4]L. Burgueño, M. F. Bertoa, N. Moreno, and A. Vallecillo, “Expressing confidence in models and in model transformation elements,” in MOD- ELS’18. ACM, 2018, pp. 57–66.
[5]M. Zhang, S. Ali, T. Yue, R. Norgren, and O. Okariz, “Uncertainty-wise cyber-physical system test modeling,” Software & Systems Modeling, Jul 2017. [Online]. Available: https://doi.org/10.1007/s10270-017-0609-6
[6]Object Management Group, Precise Semantics for Uncertainty Modeling (PSUM) RFP, May 2017, OMG Document ad/2017-12-1. [Online]. Available: https://www.omg.org/cgi-bin/doc.cgi?ad/2017-12-1
[7]E. Seidewitz, “What models mean,” IEEE Software, vol. 20, no. 5, pp.26–32, Sep. 2003.
[8]B. de Finetti, Theory of Probability: A critical introductory treatment. John Wiley & Sons, 2017.
[9]A. Critch, “Credence — using subjective probabilities to express belief strengths,” Retrieved 15 January 2019. [Online]. Available: http://acritch.com/credence/
[10]J. L. C. Izquierdo and J. Cabot, “JSONDiscoverer: Visualizing the schema lurking behind JSON documents,” Knowl.-Based Syst., vol. 103, pp. 52–55, 2016.
[11]S. Pérez-Soler, E. Guerra, and J. de Lara, “Collaborative modeling and group decision making using chatbots in social networks,” IEEE Software, vol. 35, no. 6, pp. 48–54, 2018. [Online]. Available: https://doi.org/10.1109/MS.2018.290101511
[12]W. Oberkampf, S. M. DeLand, B. Rutherford, K. V. Diegert, and K. F. Alvin, “Error and uncertainty in modeling and simulation,” Rel. Eng. & Sys. Safety, vol. 75, no. 3, pp. 333–357, 2002.
[13]Object Management Group, Unified Modeling Language (UML) Speci- fication. Version 2.5, Mar. 2015, OMG document formal/2015-03-01.
[14]——, Object Constraint Language (OCL) Specification. Version 2.4, Feb. 2014, OMG Document formal/2014-02-03.
[15]A. Hájek, “Interpretations of probability,” in The Stanford Encyclopedia of Philosophy, winter 2012 ed., E. N. Zalta, Ed. Metaphysics Research Lab, Stanford University, 2012. [Online]. Available: https://plato.stanford.edu/archives/win2012/entries/probability-interpret/
[16]M. F. Bertoa, N. Moreno, G. Barquero, L. Burgueño, J. Troya,and A. Vallecillo, “Expressing measurement uncertainty in OCL/UML datatypes,” in ECMFA’18, ser. LNCS, vol. 10890. Springer, 2018, pp. 46–62.
[17]S. Gérard, C. Dumoulin, P. Tessier, and B. Selic, “Papyrus: A uml2 tool for domain-specific language modeling,” in Proc. of MBEERTS’07. Berlin, Heidelberg: Springer-Verlag, 2007, pp. 361–368.
[18]M. Gogolla, F. Büttner, and M. Richters, “USE: A UML-based specifi- cation environment for validating UML and OCL,” Science of Computer Programming, vol. 69, pp. 27–34, 2007.
[19]F. Büttner and M. Gogolla, “On OCL-based imperative languages,” Sci.Comput. Program., vol. 92, pp. 162–178, 2014.
[20]A. Olivé, Conceptual Modeling of Information Systems. Springer, 2007.
[21]W. Feller, An Introduction to Probability Theory and Its Applications. Wiley, 2008.
[22]H.-J. Zimmermann, Fuzzy Set Theory – and Its Applications, 4th ed.Springer Science+Business Media, 2001.
[23]S. J. Russell and P. Norvig, Artificial Intelligence. A Modern Approach, 3rd ed. Prentice Hall, 2010.
[24]G. Shafer, A Mathematical Theory of Evidence. Princeton University Press, 1976.
[25]B. Liu, Uncertainty Theory, 5th ed. Springer, 2018.
[26]E. Denney and G. Pai, “Tool support for assurance case development,”Autom. Softw. Eng., vol. 25, no. 3, pp. 435–499, 2018. [Online].Available: https://doi.org/10.1007/s10515-017-0230-5
[27]B. Littlewood, M. Neil, and G. Ostrolenk, “The role of models in managing the uncertainty of software-intensive systems,” Reliability Engineering & System Safety, vol. 50, no. 1, pp. 87 – 95, 1995.
[28]D. Garlan, “Software engineering in an uncertain world,” in Proc. of the FoSER Workshop at FSE/SDP 2010. ACM, 2010, pp. 125–128.
[29]M. Famelis, R. Salay, and M. Chechik, “Partial models: Towards modeling and reasoning with uncertainty,” in ICSE’12. IEEE Press, 2012, pp. 573–583.
[30]N. Esfahani and S. Malek, “Uncertainty in self-adaptive software sys- tems,” in Software Engineering for Self-Adaptive Systems II, ser. LNCS, no. 7475. Springer, 2013, pp. 214–238.
[31]R. Salay, M. Chechik, J. Horkoff, and A. Sandro, “Managing require- ments uncertainty with partial models,” Requirements Eng., vol. 18, no. 2, pp. 107–128, 2013.
[32]P. Smets and R. Kennes, “The transferable belief model,” Artificial Intelligence, vol. 66, no. 2, pp. 191 – 234, 1994.
Antonio Vallecillo is Professor of Computer Science at the University of Málaga. His research interests include model-based software engineering (MBSE), open distributed processing (ODP) and software quality.
He has organized several international conferences, including ECOOP 2002, TOOLS 2010, MODELS 2013 and ECOOP 2017, has served as PC Chair for conferences such as TOOLS, ICMT, ECMFA, QoSA and ICSOC, and is in the editorial board for the Sosym and JOT journals. He has been Vice-President of Posgraduate and Doctoral studies at the University of Málaga (2012-2016), and the President of the Spanish Society on Software Engineering (SISTEDES) between 2014 and 2018. Since 2017 he coordinates the Computer Science and Information Technologies (INF) subarea of the Spanish Research Agency (AEI).



Nice work, Antonio.
Interesting work. My last work in a similar field here:
https://www.igi-global.com/chapter/digital-documents-as-data-carriers-and-a-method-of-data-management-guaranteeing-the-unambiguity-of-the-recorded-information/275700
What does a potential collaboration with you look like, I am an independent researcher.