Prof. Houari Sahraoui and his team in Montreal are working hard to democratize the use of genetic programming within the framework of model-driven engineering. They argue, with many others, that MDE artefacts are too complex to be written manually, which is error-prone. Since MDE offers a complete linguistic description of its artefacts, that higher-level description can be used to derive them. Following this track of ideas, Search-Based Software Engineering stands that it is easier to provide examples of an application illustrating well a problem, than to draw a general theory about how to solve it. I’ll give here an example of genetic programming, see if you get the point easier than in the textbooks.
More precisely, our last publication:
- reminds that the use of genetic programming is well fit to the learning of complex MDE artefacts, and
- shows how its execution can be significantly accelerated with genuine optimizations completely agnostic of the problem domain.
The details of our work can be found in our recent publication “Promoting social diversity for the learning of complex MDE artefacts”. In what follows, we present you a summary of our work.
In this post, I will first introduce genetic programming (GP) and then show through a simple illustrative example how a simple measure for social diversity significantly improves its efficiency (it’s breathtaking, you are warned). Though I won’t go deep into the adaptation of GP to the learning of well-formedness rules – this shall be part of a latter post – but I’ll present the results of our evaluation to assure the reader that our approach make sense, and a good sense.
Learning complex artefacts with genetic programming – Examples and semantic fitness
The use of genetic programming (GP) is not new and many, many many, studies argument on the advantages of automatically learning programs instead of writing them. It is used to help cope with growing volumes of handwritten programs of increasingly complex information.
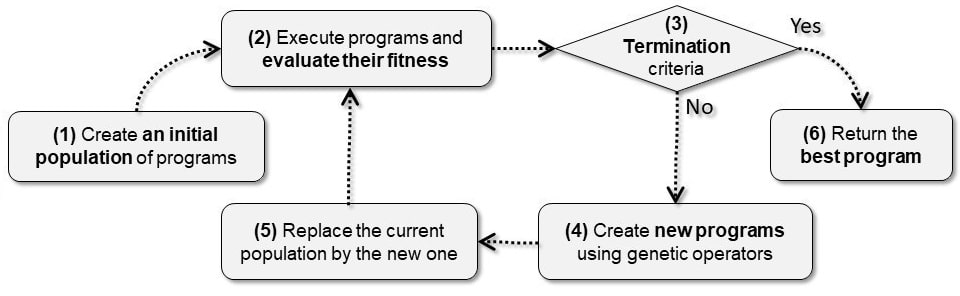
Fig. 1 schematizes a typical GP execution. First, an initial population must be provided. It is most of the time generated randomly (as randomly as it can be). The programs of this initial generation are executed, and their fitness is evaluated. If a termination criterion is reached, the set of the best programs is returned. Otherwise, individuals of the last generation are used to produce a new one using genetic operators (crossover and mutations, as mimetics of a Darwinian scheme of sexual reproduction).
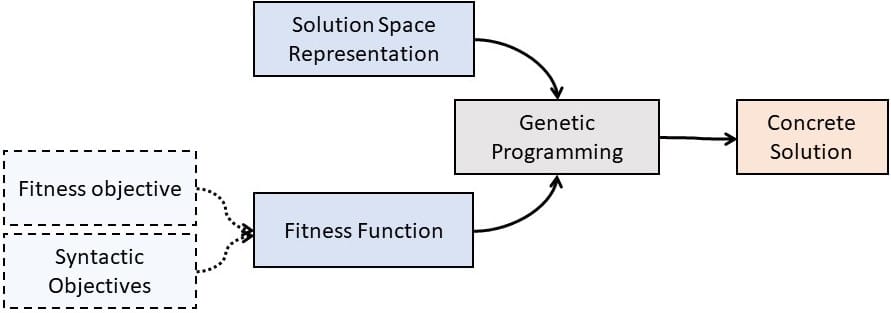
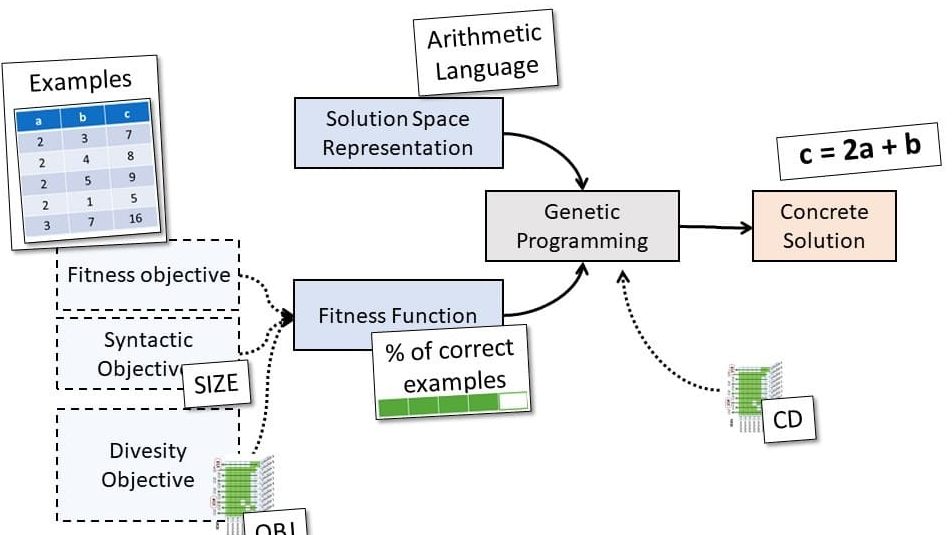
The idea of GP is to separate between the means (genetic operations on individuals) from the goal of the search (fitness of individuals). Applying GP requires one to define what a program is (what regulates its syntax) and what a good program is (what makes it fit to the problem to solve). In the same fashion as the robustness of a program can be proxied with test cases, example-based learning uses examples (and counterexamples) to measure the semantic fitness of a program. Vanneschi et al. call this an indirect semantic method that “act on the syntax of the individuals and rely on survival criteria to indirectly promote a semantic behavior”.
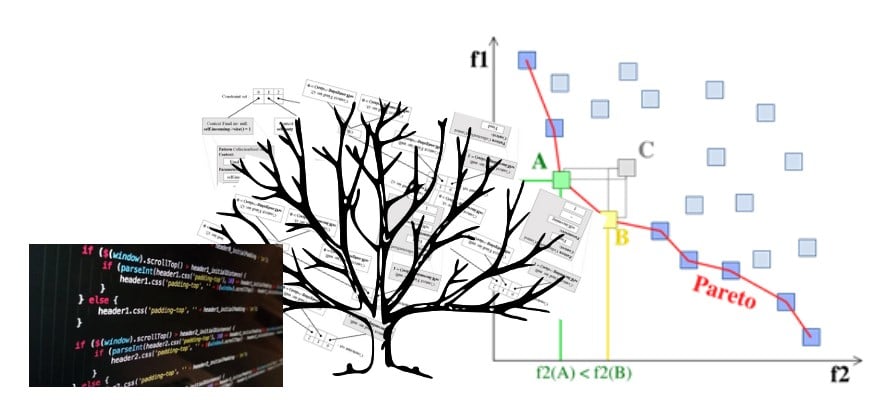
In its adaptation for Search-Based Software Engineering (Fig 2), GP derives into multi-objective GP to consider concurrently distinct objectives during the evaluation of populations. Besides a semantic fitness based on the number of examples correctly solved, it’s a common practice to add a size objective to tackle the well-known bloating effect: when potential solutions grow so big that they withhold execution from convergence and avoid meanwhile more accurate solutions.
The consideration of a size objective in parallel to a semantic fitness is particularly relevant to SBSE since it is a requirement to avoid potential solutions to grow too big and to maintain solutions as small as can be (remember that output programs should be readable by humans).
If diversity, for its part, has been largely studied, it has never been employed in the specific context of SBSE, less for its social and semantic characteristic. A pity, since SBSE offers an auspicious milieu to explore potential plus value of phenotypic diversity since the evaluation of program behavior is embedded in its core.
Multi-objective genetic programming – an Example and a limitation
We introduce here a simplified example that illustrates the idea behind our social diversity without the cognitive cost of a full-blown showcase. This example-model reduces the accidental complexity and shall help the reader better grasps the idea of the approach we used to tackle the issue.
Conundrum
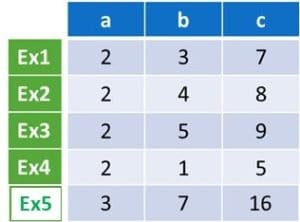
As a simple example, consider the problem that consists in finding an arithmetic expression defined by a set of examples.
The arithmetic expression takes as input a couple of integers and produces as output one integer. It is thus in the form f (a, b) = c, where f is an arithmetic function, and a, b, and c are integers. A possible set of examples that can be used to learn the arithmetic expression is shown in Fig 3. Each row in the table represents an example, i.e., a tuple of integers representing input couples with their expected output. Accordingly, the fitness of a candidate solution is the ratio of examples this candidate solves: A perfect solution will solve them all.
Solution representation
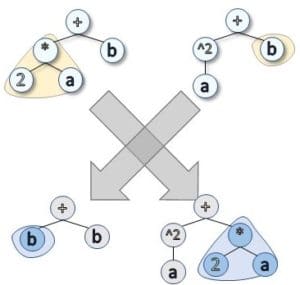
The first, and one of the most important aspect of GP lies in the representation of potential solutions. In our example, arithmetic expressions (Fig 5) can be presented as trees with math operations as nodes and values as leaves (See Fig 6).
This tree representation can be intermediary. You will find a case for complex structures in our paper, Section 2.1 Learning complex artifacts—an illustrative case, but for now, let’s simply stand that a tree representation allows for the application of genetic operators of two kinds: crossovers and mutations. A crossover consists in taking a subtree of each parent solutions and exchange them to create new offspring. A mutation consists in changing the value of a node or leaf, or of entire subtrees.
Search-based computation and the rise of Alphas
In practice, a search-based approach to learning (e.g., genetic programming) will easily find a function that solves Examples 1 to 4: for instance, as shown in Fig. 5, solution f3(a, b) = 2a + b. This easy-to-find candidate will show a fitness of 100% (4 out of 4 examples are solved).
Yet, the same algorithm might yield the same solution for the second case illustrated with the addition of Example 5. Solution f3 shows a high but not perfect fitness, 80% (4/5), illustrated in Fig. 4.
It has a fair chance to take part of the reproduction, and many other similar alpha individuals, sharing a similar behavior, will form the majority of the population. Indeed, during evolutionary computation, solutions showing a high fitness have better chances to breed the individuals of the next generation. Alphas grow numerous, and their dominance arises against candidates with a lower fitness — whose genetic material is lost through successive generations. A local optimum, or single fitness peak, is reached.
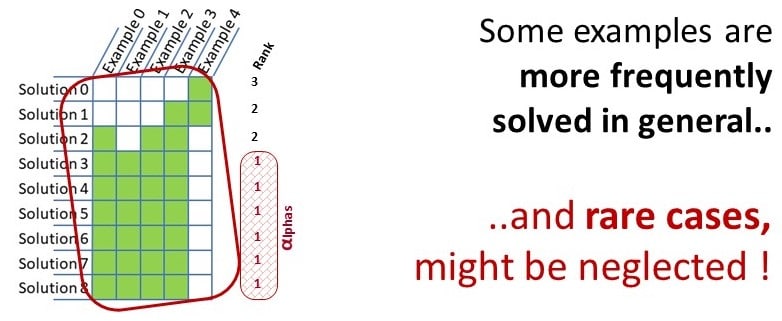
In our running example, consider the following arrangement where, among five candidate solutions, the one that could bring the necessary genetic material required to solve Example 5 is mistakenly neglected.
Typically, f0 features an interesting operator (square, in 2a2) but exhibits a weak fitness since it only solves the case of Example 5 (i.e., {a = 3, b = 3, c = 12}). Maintaining diversity shall favor the survival of this genetic material through generation and therefore potentially help with solving other cases.
Social semantic diversity
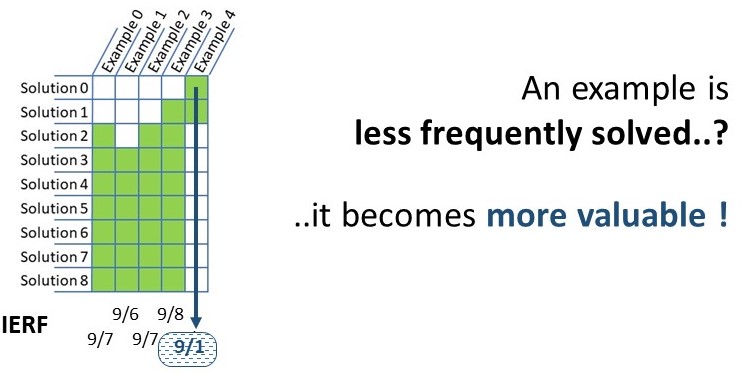
We propose a new diversity measure that prevents selection being “biased towards highly fit individuals” by an explicit consideration of individuals’ participation in the population’s behavioral diversity. Back to our running example, Solution 0, f0, solves an example that no other solution solves, Example 5, and therefore, it should purposefully be given more attention. In our approach, the weight of an example in the evaluation of an individual’s fitness is no longer absolute but varies dynamically with the geometry of the population. In simple terms, the more solutions correctly handle an example, the less this example counts in the calculation of the solutions’ fitness.
We call social semantic diversity a measure that takes into account, not the only individualistic fitness (i.e., how many examples an individual resolves), but considers as well a social dimension (i.e., what does that individual bring to the general fitness of the population).
The computation of the social semantic diversity (SSD), based on the inverse example resolution frequency (IERF), is inspired from the term frequency-inverse document frequency (TF-IDF) information retrieval technique. In pragmatical words, the SSD of a solution is the sum of IERF of the examples it solves.
Paraphrasing TFIDF definition may help the reader to grasp the general idea of SSD. We formulate it as follows: “SSD increases proportionally to the number of examples solved and is offset by the frequency of which an example is solved by the population’s individuals, which helps to adjust for the fact that some examples are more frequently solved in general.” As a consequence, SSD favors solutions solving corner cases by giving importance to candidate solutions solving examples that others do not. In Fig. 6, Example 5 is solved by only one solution and thus gains a stronger IERF than other examples. As a consequence, solutions solving this example gain better SSD and are favored for breeding the next generation.
Empirical evaluation
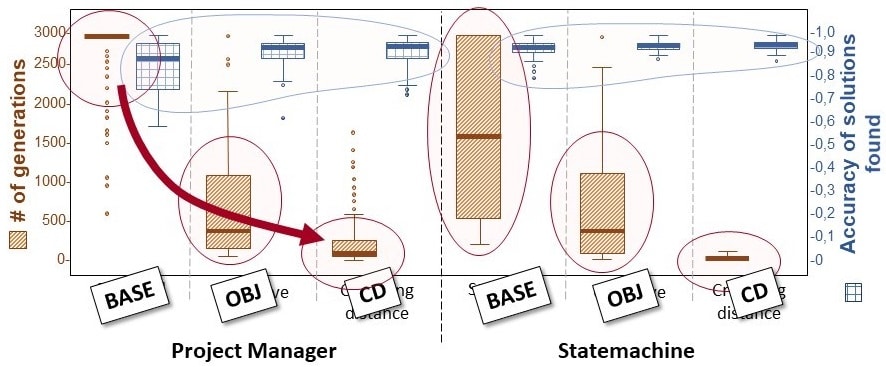
To measure the potential of our approach, we ran an empirical evaluation that compares between our three alternative configurations: the BASE alternative (i.e., without diversity measure) is compared with an implementation of diversity as a distinct fitness objective (OBJ) and with an implementation of diversity as a dedicated crowding distance (CD). The crowding distance is a mechanism from NSGA-II, a non-sorting genetic algorithm that is agnostic of the domain of application.
Using metamodels of different characteristics, we ran our algorithm hundreds of times to evaluate the speed, the convergence, and the generalizability of our approach. Speed and convergence are measured based on the duration of a run in terms of genetic operations (#GEN) whereas generalizability is measured on a test bench of examples alien to the learning set (#ACC).
We show that our approach reduces by almost 30 times the time to convergence of a run, with a steep and consistent learning curb. the use of our diversity measure not only accelerates drastically executions of GP, it also favors a better generalizabilityThis can be seen in Fig 9. In blue, the small but significant augmentation of “accuracy” shows that when tested against a new set of examples – which where not used for learning – the generalizability then augments with the use of our diversity measure. In red, the drastic cut in computation time necessary to run GP algorithms when augmented with diversity.
More, Fig 10 shows the evolution of individuals’ average accuracy value during runs on our largest metamodel with a hundred runs a plot. Subfigure a) shows a standard run without diversity measure. b) shows a steep, but randomly delayed rise of the semantic fitness when OBJ is used; c) figures how unbelievably quick the semantic fitness converges when its crowding distance alternative CD is used.
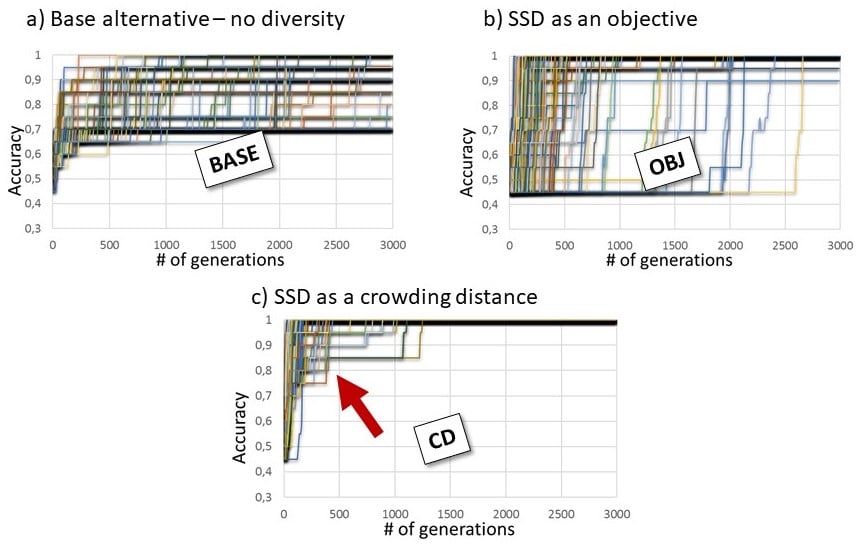
Figure 11: semantic fitness converges much faster and more consistently with social diversity measure
Conclusion
This work was part of an investigation on the learning of well-formedness rules for scientific purpose. Software fundamentals, with a perspective from the modeling community. I enjoyed it because it involved a clear understanding of the mechanisms at work when GP is performed. In other words, we had to model the genetic mimesis and its executions to find the optimization we show here.
Genetic programming has been somehow despised by the prominent use of deep and other neural approaches to learning. Buzzwords rampage scientific research. Yet, the direct manipulation of complex artefacts is unique to GP and it goes in a similar way as nature do – or at least following a broadly shared common understanding of evolution. And now, it goes fast(er) !
After years implementing and optimizing GP for the learning of well-formedness rules, model transformation, refactoring, code smells… we believe that the idea to consider the social dimension of individuals’ characteristics shall apply to the evolutionary computation of these other complex artifacts.

Edouard is a postdoctoral fellow working in the SOM Research Lab at the Internet Interdisciplinary Institute (IN3) of the Open University of Catalonia (UOC) in Barcelona. His most prominent expertize lies in the use of machine learning to derive complex engineering artefacts by means of usage examples.
Currently working on the conjunct use of AI and MDE for certification traceability purpose, his topics of interest span from software modelling engineering and quality to the social and political consequences of ubiquitous technologies.
You will find Edouard’s complete curriculum here or interact with him by email: ebatot [at] uoc [dot] edu.

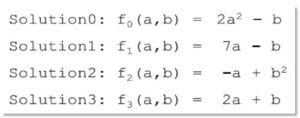


I researched on both layered back-propagation networks and genetic algorithms a 25+ years ago.
Based on that experience I state, genetic algorithms is a viable approach in this domain.
Many, many thanks for sharing.
/Carsten
Thanks for your support Carsten.
Truth is, this little change in the evolutionary algorithm changed my life while graduating. I used to run thousands of ghost executions on a dedicated server to try-and-test my configurations – that would last sometimes up to two days… With that little tip I could run it in less than an hour. That was a must – seeing the curb drawn real time in from of my eyes was mindblowing 🙂
Thanks,
Edouard