During the OCL Workshop at MoDELS 2016, Daniel Calegari and Marcos Viera presented the idea of using the functional paradigm for the interpretation of OCL expressions (full paper available here).
The idea generated plenty of discussions so I invited them to expand on the concept of OCL Monads, the functional interpretation of OCL and its benefits. In what follows, we briefly resume the idea and provide some insights on its benefits. Enter Daniel and Marcos.
Since its origins, the OCL was defined as a declarative side-effect free language, combining model-oriented and functional features, e.g. type inheritance and functions composition, respectively. In the last few years, other functional features were proposed for their inclusion in the new OCL version, e.g. pattern matching, lambda expressions, and lazy evaluation. In this context, a functional approach comes as a reasonable alternative for exploiting such features. As a first step, we explored the use of Haskell as an interpreter for OCL with respect to its use for expressing invariant conditions in models, in the context of the Model-Driven Engineering paradigm.
Functional Representation of (meta)models
The functional interpretation of OCL requires, first, to tackle the functional representation of metamodels and models, which introduces some sort of model-functional impedance mismatch. Metamodels are represented as data types, and models conforming those metamodels are values of the type representing the metamodel. However, functional data types are tree-like structures, thus, each model element needs to have an identifier, so that references between elements (in a graph-like fashion) are expressed using such identifiers.
Without delving into details, the next fragment shows an excerpt of a functional representation of a metamodel in which there is an UMLModelElement with two attributes kind and name, an Attribute with two references to a Classifier and a Class. Each element is represented as a data type with their corresponding attributes. Moreover, the superclass contains an identifier oid, and references are expressed based on the identifiers.
-- UMLModelElement(oid:int, kind:String, name:String) data UMLModelElement = UMLModelElement Int String String -- Attribute(typ:Classifier, owner:Class) data Attribute = Attribute Int Int |
Functional interpretation of OCL
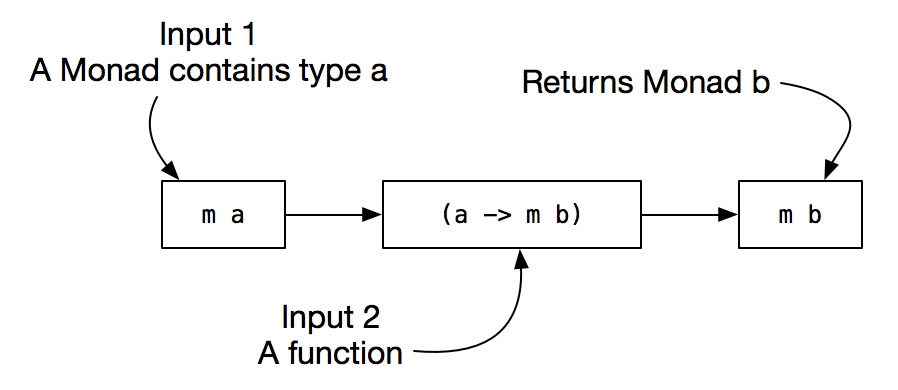
The complex part of the interpretation comes when dealing with model-oriented features on OCL expressions (e.g. type casting and navigation through properties) which require accessing the information of a specific model, and to perform a chain of computations. Moreover, we have to deal with the four-valued logic behind OCL with the notion of truth, undefinedness, and nullity. These aspects were handled by defining an OCL Monad.
Within the functional paradigm, a Monad is basically a structure which represents computations in terms of values and sequences of (sub)computations that use these values. In particular, the Reader monad is a special kind of monad representing computations over a shared environment.
Our proposal is based on representing every OCL expression as a computation over a Reader monad such that the shared environment corresponds to the model over which the OCL expression is specified. The monadic operator bind, defining a sequence of computations, allows representing navigation through properties and functions, such that the result of a computation is linked to each subsequent computation within the monad. Since we represent the result of a computation with a special type dealing with the OCL four-valued logic, after each computation we have the OCL Monad with the shared environment unmodified and the corresponding value at the moment of the computation.
This solution allows a clean handling of errors and a precise definition of the four-valued semantics of OCL. Moreover, it allows a direct representation of the OCL invariants mimicking its structure in a clear way. Without delving into details, the next fragment shows that the OCL invariant and its corresponding functional version are very similar.
context Classifier inv: self.oclIsTypeOf(Class) implies self.oclAsType(Class).attribute->size() > 0 chk = context Classifier [inv] inv self = (ocl self |.| oclIsTypeOf Class) `implies` ((ocl self |.| oclAsType Class |.| attribute |->| size) > oclVal 0) |
Some final thoughts
This approach is exploratory. However, it provides some benefits.
First, although the functional infrastructure we need for expressing invariants could not be easily readable for an inexperienced user, some parts can be predefined (the whole OCL library is model-independent) and the other automatically generated (e.g. operations for accessing model properties).
Second, it is potentially extensible for other OCL uses, e.g. for the description of pre- and post-conditions on operations and for constraining and computing object values in the definition of model transformation.
Finally, we like to think about this approach not as a potential contender of industrial tools, but as a “sandbox” in which functional abstractions can be used in order to evaluate many proposals that the community already made. Moreover, we hope this can help with the migration of functional concepts to the model-driven world.
Featured image taken from the Yet Another Monad Tutorial in 15 Minutes
FNR Pearl Chair. Head of the Software Engineering RDI Unit at LIST. Affiliate Professor at University of Luxembourg. More about me.



You introduce a Monad for the ‘4-valued’ logic of constraints.
Arguably since constraints have a 2-valued result, the 2-valued characteristic can be pushed back by null/invalid analysis to ensure that all Boolean computations are 2-valued; presumably rather simpler.
But ‘4-valued’ is a regular misnomer. Every N-valued type in OCL has an N+1 and N+2 valued variant to accommodate null and perhaps invalid. Do these work comfortably with Monads or does the OCL type system need revisiting?
You are right. We did not give much details, but in fact we implemented the N+2 valued variant of any type by wrapping the values by a data type:
data Val a = Val a | Inv | Null
Thus, if we have for example integers, the computation can return a valid integer (e.g. Val 4), invalid (Inv) and null (Null). This solution is not only extensible but also allows the use of OCL in other contexts (yet unexplored).
Just for the record, as I’m sure the authors know, the ‘standard’ way of doing this is as a product where the right side represents a ‘correct’ (i.e. right) value, and the left side (‘sinister’ in Latin) represents an exceptional value. In this case, the left side would be a choice (i.e. sum type, coproduct) between Inv and Null. Example: http://try.purescript.org/?gist=e43ec1103ed9fa74234e7e284f5da4f5