Objects and Relations in Scrall

Today is the day that we address the R in Scrall.

And this week’s blog is brought to you by The Matching Half Cafe in San Francisco where I write in the mornings. They aren’t actually sponsoring me, but I thought I would give them a shout out anyway since they are so awesome. They have fresh homemade poptarts, non-wobbly tables, slightly wobbly wireless, top-notch caffeine and intermittent scenery wandering in after yoga class. I don’t think it gets any better than this.

Ok, back to relational something or other…

The key distinction of the sm UML branch of executable UMLs is its firm relational foundation. Just like light is both a wave and a particle in physics depending on what kind of problem you are trying to solve (even though it is really particles either way), an sm UML class is either a class or a relation (table) depending on your goals. And, mathematically speaking, it is most definitely a relation either way.

We are talking about platform independent model semantics here and not implementation. It is, in fact, the strict mathematical foundations that free us to implement any way we want, object oriented or otherwise, which is so important for embedded system platforms.

When objects are good

Objects are great for a lot of things. We like to send them signals for example:

Wake up -> /Child
!notarget:{
   // alternative actions if no objects selected
}

That, by the way is the signal sending notation. The Wake up signal is delivered to all Child objects, if any. The optional exception clause prevents any attempt to send if no objects are selected. Signal sending and exception handling are mentioned only in passing in this week’s post.

Objects are also useful stepping stones for navigating relationships when the path is relatively smooth. Object oriented manipulations are fine for simple computations such as accessing and updating an attribute value here and there. And, of course, objects also have all those groovy methods you can invoke on them. So we like objects!

When relations are better

But when it comes to more complex computing, as we do in state and method activities, we are less concerned about the objects as active entities and primarily interested in the various data values that correspond to those objects.

When we traverse relationships sometimes we want to go ‘off-road’ and tear up the attribute flower beds. Sometimes we want to break a class up into its constituent data and then recombine it with data from related classes in novel ways to discover useful facts. If we limit ourselves to object-oriented thinking we end up with a lot of nested loops and action language doing all kinds of unnecessary procedural gymnastics. This, in turn, can funnel our implementation choices into needlessly sequential processing requiring more code than we truly need.

Unfortunately, the tools that support sm UMLs tend to highlight the object-oriented manipulations, hiding and virtually apologizing for the relational foundations so as not to alienate or confuse the poor object-oriented developer. It has been my experience that developers are on the whole rather smart and adaptable folks eager to learn new methods and technologies. Honestly, if you can figure out how to code well in C++ or Java, this relational algebra thing is a piece of cake. I mean, there’s only ONE data structure, how hard could it be?

I will demonstrate what I mean with a dramatic OAL / Scrall comparison. But first, I need to introduce the building blocks we need to access the power of relational algebra that has always been lying, untapped at the heart of sm UMLs. Today we unleash the beast!

Object, Scalar and Relation values

In Scrall, we deal with three distinct kinds of values. We’ve already covered object reference values which we store in object variables. And you are well familiar with data values such as temperature, position and speed which can be defined with arbitrary nested structure in most programming languages. In Scrall, as in the relational world, we refer to these as scalar values to distinguish them from relation and object values. Relation values (a relation is a value, so you can just say ‘relations’) are defined formally in relational theory and we can store them in a special kind of variable. All three variable types are local in scope to the activity in which they are defined. Classes and attributes represent the only data persisting across activities.

Relations

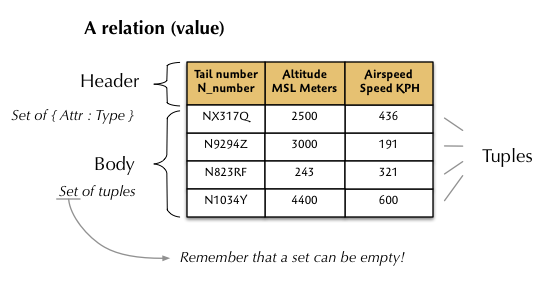
Here is an example relation:

It consists of two parts, a heading and a body. The heading is defined as a set of zero or more attribute, type pairs. The body is a set of zero or more tuples. Each tuple is a set of values where each value corresponds to an attribute in the heading.

While a relation can usually be viewed as a table, this is just a convenient illusion. For example, the horizontal attribute order and the vertical tuple ordering has no significance. So the following relation is equivalent to the one above, even though the table representations are clearly different.

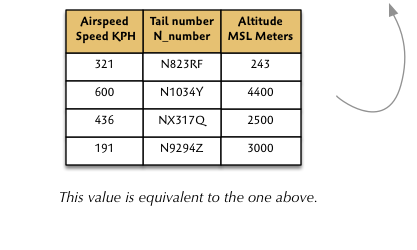
The relation is what’s important, not the table. A more accurate way to view a relation is as a collection of sets, like this:

Relation {
Heading { Altitude : MSL_Alt, Airspeed : Meters per hour }
Body { { Altitude : 3000, Airspeed : 200 },
   { Altitude : 4200, Airspeed : 218 } }

And, good luck drawing a table for these two relations:

Relation { Heading {}, Body { {} }  // (true)
Relation { Heading {}, Body { } // (false)

The first relation above has a heading with no attributes and a body with one empty tuple while the other has zero attributes and zero tuples. When returned as results from a relational operation these two relations are regarded as logical true and false. So I think I’ve made my point that a relation is not necessarily a table, but a tabular format is often convenient way to view a relation. Furthermore, there is no expectation that any kind of table-ish data structure is required for implementation.

THAT SAID, I would like to introduce the table variable which we use in Scrall to store a relation. (I wanted to use the term ‘relation variable’, but the relational folks use an abbreviated version, ’relvar’, to describe what we think of as a ‘class’).

Defining a table variable

Use the table #= assignment operator to define and initialize a table variable. It should be easy to remember since the # character resembles a table.

acdata #= Aircraft // init with all Aircraft objects

Since no selection criteria or attributes have been specified, data from the entire object population of Aircraft is used to initialize the acdata table variable. So the value of that variable might look like the relation pictured above.

Tuples to objects

You can convert the value of a table variable to one or more object references if the table variable heading is an identifier of some class. But you need to specify the class.

Aircraft::slow aircraft ..= acdata(
   Airspeed: < low speed ).Tail number

The expression on the right hand side selects all tuples with a low Airspeed value and then projects out just the Tail number values. Since Tail number is an identifier of Aircraft, indicated on the left hand side, the appropriate object references can be populated into the slow aircraft object set variable.

Tuple attribute value to a scalar value

If you have a single tuple relation, you can extract data to initialize a scalar variable.

my acdata #= /is flying/Aircraft.(ID, Altitude, Airspeed)

Let’s say the association to Aircraft is one conditional (0..1). That means that we also need to verify that there is a single tuple in the relation. The #1and #0 unary cardinality operators work on both table and object variables to return true if there is one or zero object/tuples respectively. Then, combined with a conditional assignment, we can extract the Airspeed as a scalar value.

my airspeed = my aircraft.Airspeed if #1 my acdata \
    else default airspeed

The default airspeed variable is a scalar variable initialized earlier.

There is one more unary cardinality operator # that returns the number of tuples in a table variable or the number of objects in an object variable, so you can do:

qty slow aircraft = #acdata


Relational operations

There is just not enough blog scrolling space to demonstrate all of the relational operations that you can perform in Scrall. But just to give you a feel for things, here are some relational statements you can use.

r #= a #^ b // intersect
r #= a #u b // union
r #= a #- b // subtraction  // set complement
r #= a #* b // multiplication
r #= a( attr1: > some value ) // restriction (selection)
r #= a.( attr1, attr2 ) // projection
r #= a.( attrX@attr1 ) // rename (attr1 becomes attrX in r)

There are a couple of other operations that we need which we will use and explain in the big example.

The Component Test Example

We now need a class model with interesting associations where we can’t easily hop directly to the data we need in the usual object oriented way. Before diving into the model, let’s take a look at an example scenario first (as always!).

We are testing Components in a factory environment. There are a number of Test Stations spread out on the factory floor and there are well defined Paths leading from one Test Station to another. A Component will undergo a series of Tests at a particular station. The test sequence and dependencies are not relevant to this exercise so they are omitted.

A Component may not proceed to the next Test Station until certain Tests have been passed. Sometimes there are multiple Paths leading from one Test Station to another and the Path chosen depends on which Tests are passed by the Component. Assume, for this exercise, that at most one Path from a given Test Station can be enabled at a time (even though I haven’t modeled this particular constraint). Here is a diagram of the situation for a given scenario.

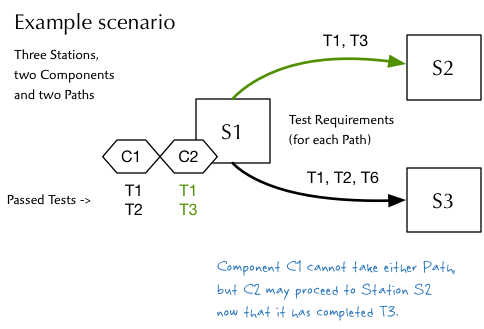
In the scenario above, Component C1 has completed two Tests at Test Station S1 but there is no outgoing Path that is enabled for it yet. Component C2, on the other hand, has just completed Test T3 and that enables the Path to Test Station S2.

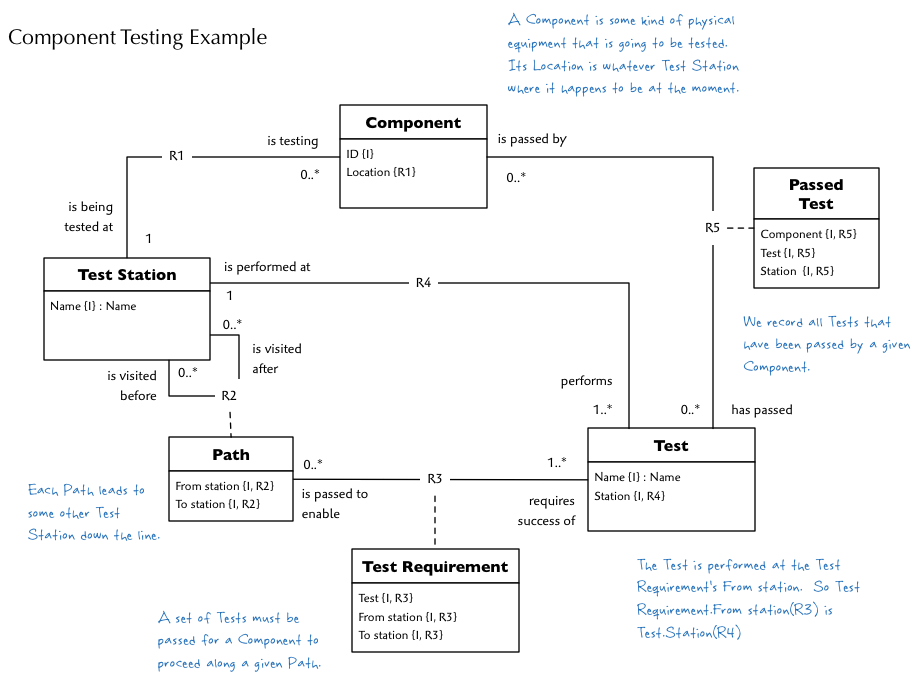
There isn’t much space for the class diagram here but I will try to squeeze it in below. Here is a link to a PDF if you have trouble reading it here.

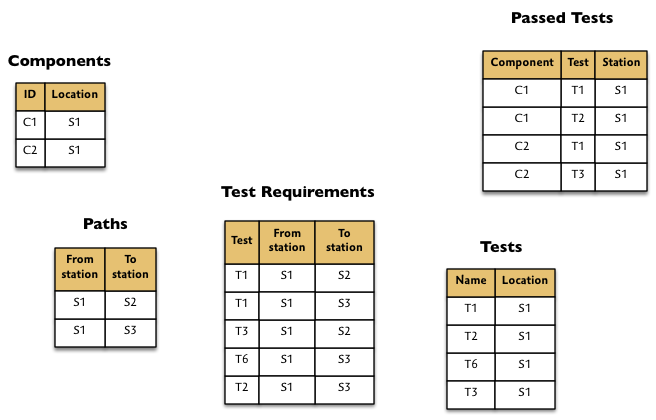
Here are some tables of the scenario data:

Here’s our problem. As soon as a Component passes a Test it checks to see if it can take an outgoing Path. If it can, it does. Simple as that. Here is the BridgePoint OAL that accomplishes the task.

// Local class is Component

select many out_paths from self->Test_Station[R1]->Path[R2];
for this_Path in out_paths
   enabled_path = true;  // assume all required tests passed
   select many path_reqs related by
       this_Path->Test_Requirement[R3];
   for this_req in path_reqs
       select many passed_req related by this_req->Test[R3]->
           Passed_Test[R5] where ( selected.Component == self.ID
           and selected.Station == this_req.From_station );
        if empty( passed_req )
            enabled_path = false;  // found a test not passed
            break;  // try another path
        end if;
    end for; // this req
    if enabled_path
        unlink self from Test_Station across R1;
        link self to 
            this_Path->Test_Station[R2].'is visited after';
        break; // Assume there are no other enabled paths
    end if;
end for; // this path
// If we get this far, no outgoing paths were enabled
    
   

Holy crap! We need two nested for-each loops, a boolean and a lot of hopping around just to compare all the outgoing Test Requirements against Passed Tests to see if any Path is enabled.

The object-relational solution

Thanks to the closure property of relational algebra, we can get all this done in just a few lines of action language without any loops or other procedural artifact. Since every relational operation returns a relation, you can nest operations to create powerful expressions, just like you can with ordinary arithmetic.

First let’s review our strategy from a relational perspective. Each time a Component passes a Test it checks to see if any outgoing Path is now enabled. The enabling condition for any outgoing Path is that its set of Test Requirements is equal to those completed by the Component at the current Test Station. For example, we would perform these set equivalence comparisons for Component C2:

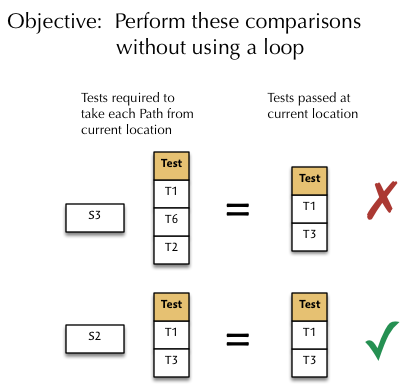
To achieve our goal, we will need to introduce two more relational operations, EXTEND and IMAGE, which we will use in combination. Let’s first see how they work individually and then we’ll put them together.

EXTEND relational operation

EXTEND is useful for performing computations. The basic idea is that you add an attribute to a relation and then compute the value of that attribute, for each tuple, using some expression that yields a value of the attribute’s type.

Let’s say, for example, that we want to compute the remaining flying time for all aircraft in flight and determine which of those need to land soon. We could do this:

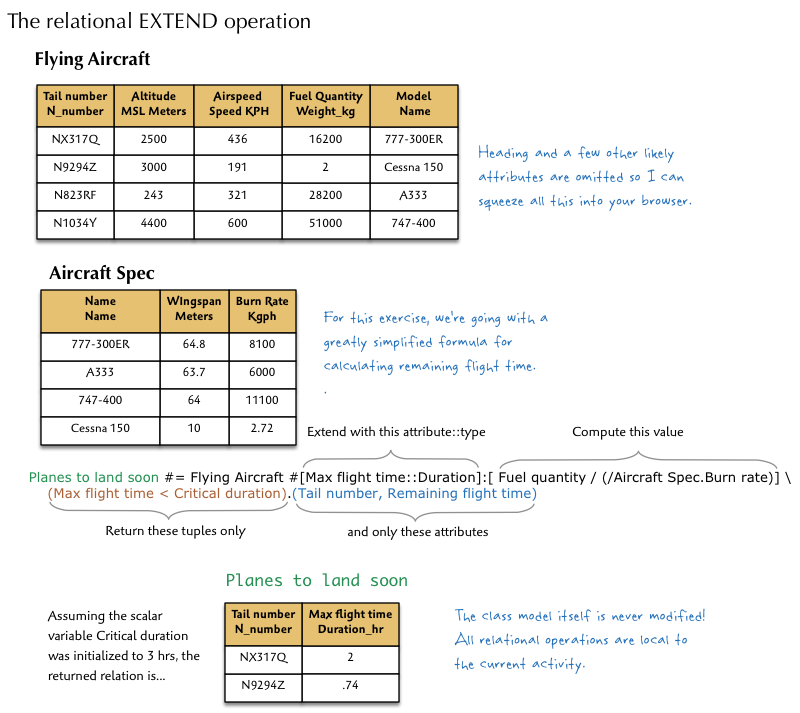
Remember that all relational operations are transient. They never change the class model structure. The Scrall syntax is:

<class> #[<attr>::<type>]:[<expr>]

The ::<type> is optional if it can be determined by the <expr>. Since EXTEND returns a relation, like all relational operations, you can tack on a selection expression and specify attributes to select or ignore using the ( <select-expr> ).( <attr-list> ) notation we’ve been using.

For our test component example, we could use the EXTEND operation to add a boolean Enabled attribute to a relation containing only destination Test Stations reachable from a Component’s current location. The trick is to compute the true/false value based on the set comparisons shown above in our objective. For that we will need the IMAGE relational operation.

IMAGE relational operation

For any given tuple in one relation, you can produce its image in either the same or, most typically, a different relation assuming there is at least one common attribute. Here is an example:

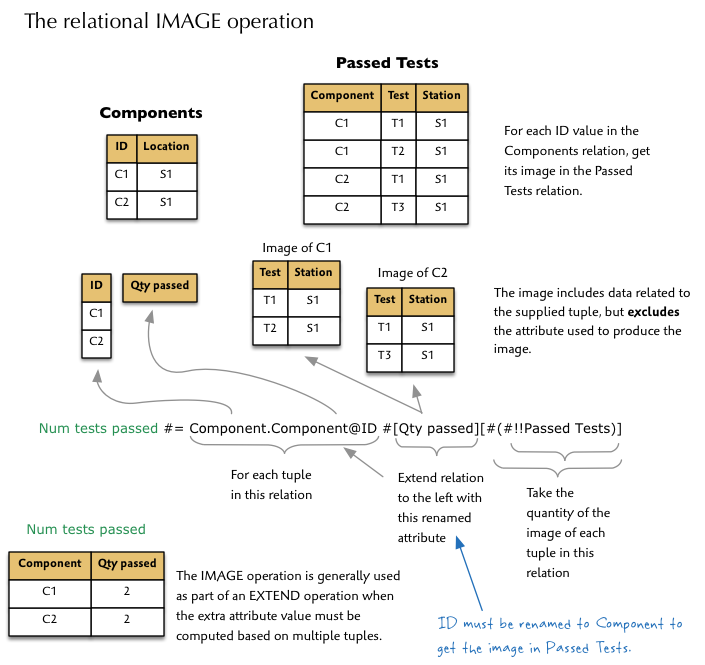
Now, the solution

Now we have everything we need to execute our strategy. First we need to create a relation with all Tests passed by the Component at its location.

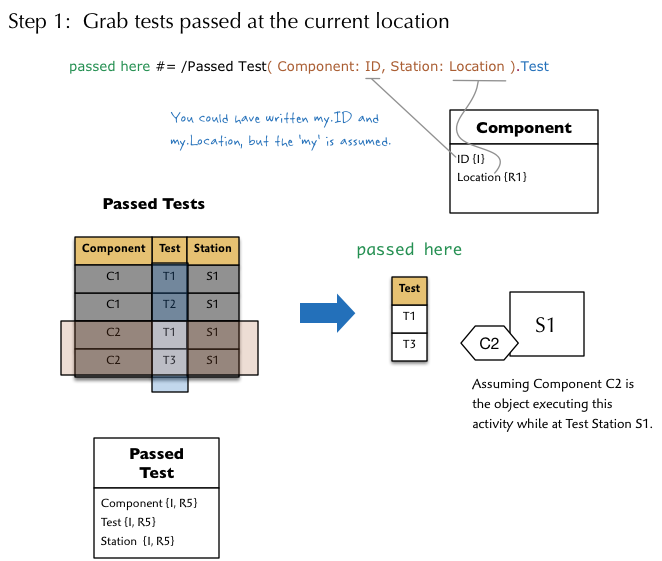
Then we need to isolate all Test Requirements that must be passed to exit the Component’s current Test Station location.

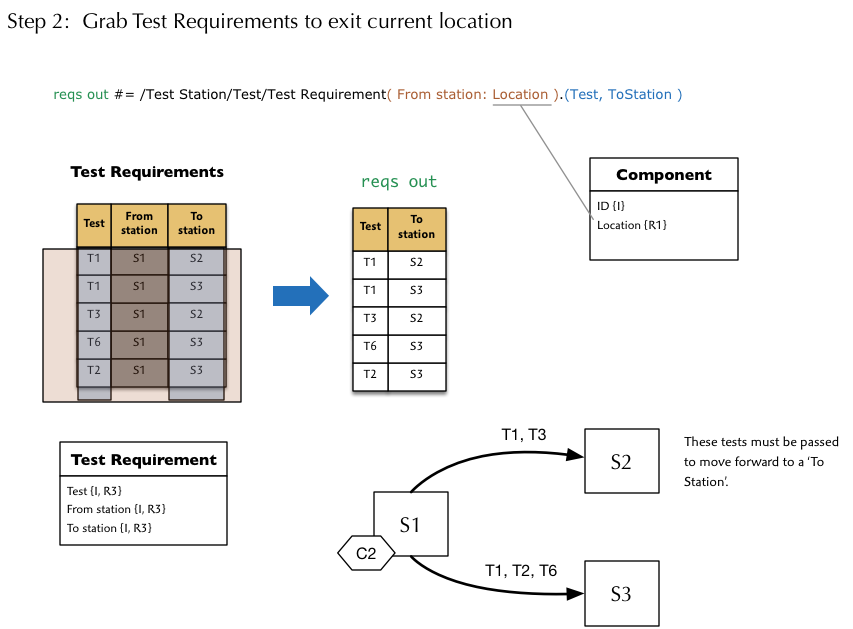
Finally, we apply the extend and image operations to find the enabled Paths.

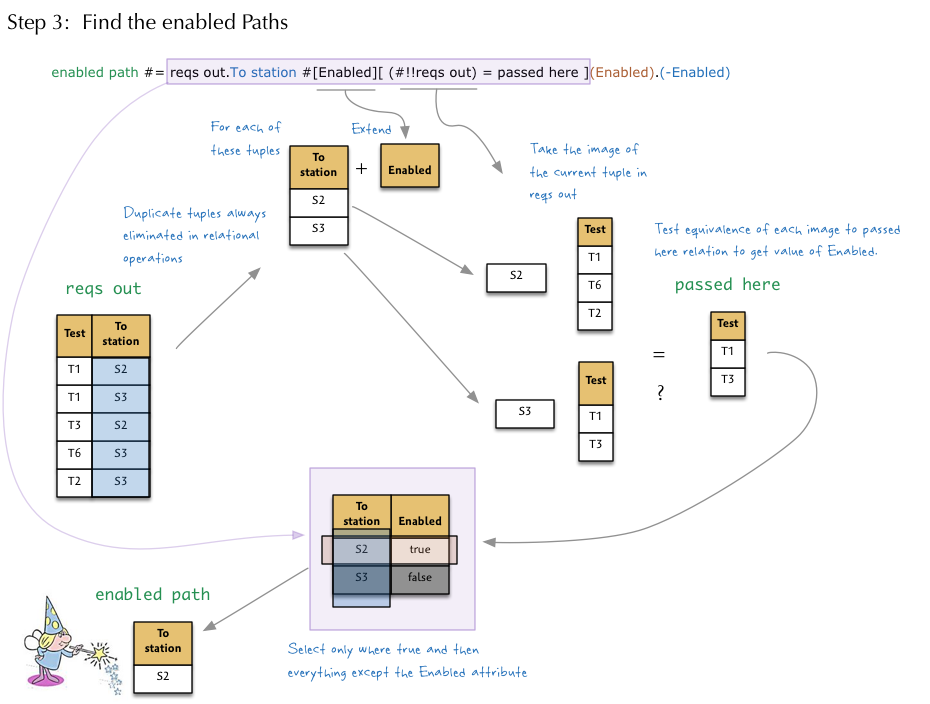
To summarize the above diagram, we first grab all the Passed Tests for the local Component object. Then we grab all the Test Requirements on the outgoing Paths. Taking only the To stations, we will EXTEND that relation with a boolean Enabled attribute. To compute the value of that attribute for each tuple, we take the IMAGE of the tuple in the very same relation to yield a set of Tests for each To station. Then we compare that to the Tests already passed by the Component. If the sets are equal, the value is true, otherwise false. Finally, we take only the To station attribute to yield the one destination, if any.

We can tighten this up a bit by converting the enabled path relation result into an object. But we do need to rename the To station attribute to Name using the @ rename operator so that it matches the identifier of Test Station.

passed here #= /Passed Test(
   Component: ID, Station: Location ).Test
reqs out #= /Test Station/Test/Test Requirement(
   From station: Location ).( Test, To station )
Test Station::new station .= ( reqs out.To station #[Enabled]
   [(#!!reqs out).Test = passed here](Enabled).(Enabled)
).Name@To station
link to new station !missing link:{ // don't advance }

That last statement effectively advances the Component by linking it (and implicitly unlinking the old location) to the new station object reference. That is, unless the variable is empty, in which case the missing link condition is first detected so that no link is attempted.

Future posts and coffee mugs

Well, that’s it for this week’s post and I hope it was worth the read. I think I will be writing just one more post on Scrall sometime later this month before moving on to other topics for a while. But I will be discussing the elimination of literal values and maybe a bit more about model level exception handling in the next post. When it is ready, I will post a link to a full specification of Scrall, including a formal grammar, later this year. Don’t be surprised if the syntax shifts around a bit by then.

And, if you want a truly unique modeling language inspired coffee mug to perplex and annoy your colleagues, feel free to take a look at some of my designs here. And, as always, please visit our Model Integration site, twitter and facebook page and say hello.

——