Managing Belief Uncertainty in Models

There are numerous domains in which information systems need to deal with uncertain information. These uncertainties may originate from different reasons such as vagueness, imprecision, incompleteness or inconsistencies; and, in many cases, they cannot be neglected.

In this blog post, we briefly present our work recently published in the ACM Transactions on Software Engineering and Methodology (TOSEM) journal, where we present our approach to represent and process uncertain information in domain models, considering the stakeholders’ beliefs (opinions). We show how to associate beliefs to model elements, how to propagate and operate with their associated uncertainty so that domain experts can individually reason about their models, and address the challenge of combining the opinions of different domain experts on the same model elements.

The goal of our work is to provide a mechanism to come up with informed collective decisions. This work complements some of our previous works on model uncertainty such as this one or this other one. You can get the full paper here [6] or read on for an extended summary.

Introduction

Information systems in domains such as archaeology, history, geography, biology, Internet of Things (IoT) or Artificial Intelligence (AI) have to deal with data that is sometimes missing, inaccurate, vague or even inconsistent due to unreliable sources, lack of knowledge, or imprecise information. In information systems, domain modeling is an important activity where the key concepts of a domain are captured. Therefore, the uncertainty that is intrinsic to a domain must be captured when experts build their models.

Current proposals for dealing with uncertain information in models tend to explicitly associate a degree of uncertainty to the affected instances, which can come from statistical analysis, trust on the sources, or even beliefs. One particular type of degree of uncertainty can be captured by the so-called degree of confidence. Degrees of confidence are normally expressed either as a probability (also called credence) or as a fuzzy quantifier (certain, probable, possible, etc.). In addition to representing uncertainty about the information, it is necessary to enable reasoning about these enriched instance models (also called object models, or object diagrams in UML terminology) when different degrees of uncertainty coming from different sources to be combined. This is desirable, for instance, in cases in which various experts (users, stakeholders, modelers, etc.) express their beliefs on model elements and need to merge them to reach agreements, or at least compromises, about the final instance model.

Our proposal aims at addressing these issues. First, we use Subjective logic [1] to express the opinions of the domain experts. Each opinion is composed by four values that are defined on an instance model element. These are:

1. the prior probability of the opinion (which is an objective uncertainty – also called initial degree of uncertainty);
2. the degree of belief ;
3. the degree of disbelief; and
4. the degree of uncertainty (in this case, this is a subjective uncertainty that reflects up to what extent the domain expert is unsure and does not have any belief or disbelief).

All these degrees are real numbers in the range [0..1]). Second, we show how more than one opinion can be assigned to one element without altering the domain model definition. To accomplish this task, we have used the UML notation. We represent domain models by means of class diagrams, and have defined a UML profile to enrich instance model elements with the opinions held by the domain experts. We have also created a set of operations to deal with opinions (e.g., propagate their associated uncertainties through operations such as and, or or xor). Third, we use the Subjective logic fusion operators to combine the opinions from different domain experts into a consensus agreement, or at least into a single compromise opinion.

Motivating example

Let us assume that we have a system whose users receive information from sensors and other external data sources that are not completely reliable or may contain inaccuracies, and therefore have an associated uncertainty such as a smart house.

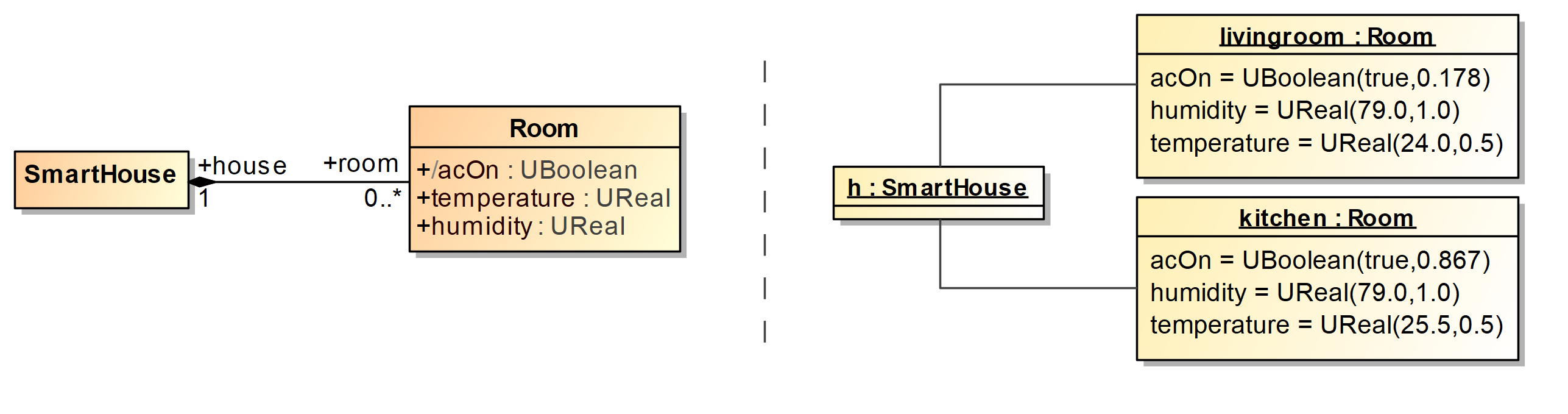
The smart house’s rooms are equipped with sensors that measure their temperature and humidity. According to their manufacturers’ information, the accuracy of the temperature and humidity sensors are ±0.5 degrees and ±1.0%, respectively. Note that this uncertainty is objective and does not come from personal (and, therefore, subjective) impressions or experiences. A control device in the room decides whether the Air Conditioning (AC) system should be turned on or off depending on the values of the sensors’ measurements. If the temperature is higher than 25 degrees or the humidity in the room is higher than 80%, the air conditioning will be automatically turned on. If this condition is not met, it should be off. The diagrams in Fig. 1 show the domain model of the system as a UML class diagram (left), and an object model that describes a house and two of its rooms (right).

The condition that establishes when the air conditioning is turned on or off is given by the following OCL expression:

acOn : UBoolean derive = self.temperature >= 25.0 or self.humidity >= 80.0

Note the use of the UML extended datatypes UReal and UBoolean that represent Real and Boolean values enriched with uncertainty [2]. Type UReal extends type Real with measurement uncertainty, enabling users to represent and operate with values like 3.0 ± 0.01, which is simply written as UReal(3.0,0.01). Type UBoolean implements the probabilistic logic extension to Boolean logic that uses Bayesian probabilities to represent the likelihood of a value to be true. A UBoolean value is a pair (b, c) where b is a Boolean value (i.e., true, false) and c is a real number in the range [0..1], representing the confidence that b is certain by means of a probability. The extended type system takes care of propagating the corresponding uncertainty through the OCL expressions.

In the particular case of the values of attribute acOn, the uncertainties are propagated through the operators >= and or. Assuming a threshold of 0.5, where a UBoolean(true,c) with c>=0.5 corresponds to the Boolean true and c<0.5 corresponds to the Boolean false, in view of the object model shown in Fig. 1, the AC system of the kitchen will be switched on while that of the livingroom will be turned off.

Once again, note that this derived uncertainty also has an objective nature since it is based on facts and derived from them. Unlike this scenario, there are many situations in which the users of such systems also associate a subjective uncertainty that coexists with the objective uncertainty of the sources. For example, let us assume that one of the house occupants, Bob, does not trust the temperature readings of the kitchen because he knows that the sensor is close to the oven and therefore the measurements are occasionally unreliable. Bob would add some subjective uncertainty to the objective results of the sensor’s measurements. This type of subjective uncertainty assigned to the same sensor by different users can vary, depending on their personal history, experiences and convictions—e.g., their individual level of trust in the sensor manufacturer. Thus, other occupants may have different opinions, or trust, on the sensors’ readings which will consequently affect their decisions on whether to switch on or off the AC system of a room. This type of uncertainty is typically called second-order probability or second-order uncertainty in the literature of statistics and economics, and needs to be captured, explicitly represented, propagated, and considered to make informed decisions about the system and the actions to take.

To further complicate matters, in most systems, users do not exist isolated, but exchange information and interoperate with each other to achieve their goals. In our example, if Ada, Bob, and Cam are occupants of the house and they hold different beliefs about the reliability of the sensors readings, how can they reach a consensus about when to turn the AC system on or off?

Research Questions

To address these issues in an orderly and systematic manner, this paper aims at answering the following research questions:

• RQ1 How can stakeholders capture and explicitly represent their opinions about the instances of domain models?
• RQ2 How can stakeholders reason about the opinions specified in the instance models and make informed decisions?

To answer this research questions, our work is supported on Subjective Logic [1] and UML Profiles. We refer the reader to the background section of our paper [6] for more information about them.

A Belief Uncertainty UML Profile for Expressing Subjective Statements

To enable users to express their opinions about particular model elements, we have created the UML profile that the following figure shows. Let us explain its elements.

First, the stereotype «Agent» is used to indicate those entities that hold opinions, which can be domain experts, users, modelers or any other stakeholder. The stereotype «UncertainElement» is used to mark any element of an object model as uncertain, and enables the assignment of degrees of belief to it. For this, the datatype Belief represents a pair (agent:Agent, opinion:SBoolean) that describes the agent holding an opinion, and the opinion held by that agent. A set of beliefs can be associated to an uncertain element, which allows different agents to express their opinions about the same model element. The stereotype «UncertainElementFusion» extends «UncertainElement» by adding a set of derived tags. Each one computes the corresponding fusion operator on the list of opinions stored in the tag beliefs of the «UncertainElement» stereotype (see below).

This profile is used to assign degrees of belief to instances, to links and to attributes’ values. In the former case, the degree of belief expresses the opinions of the agents about the actual occurrence (or existence) of the instance. The same holds for links (i.e., association instances), which express the agents’ degrees of belief about the actual existence of the relationship that the link represents in the system. When applied to attributes’ values, an opinion must be interpreted as the opinion that the agent has about the truthiness of the value of the attribute (not about whether the attribute should exist or not). In the case of derived attributes, whose values are automatically computed by OCL expressions, their opinions will be automatically derived by propagating the agents’ opinions on the operands through the expression’s operators. Thus, agents do not need to explicitly assign opinions to derived attributes. When an opinion is assigned to a link, the existence of the two related objects is assumed. This means that an opinion on a link represents a conditional opinion (in Subjective logic terms) hence the independence between the opinions about the objects and about the existence of the link between them is achieved.

This simplifies the interpretation of the object model and also the calculations when propagating the belief uncertainty, since the opinion on the links and those on the related objects are independent, and thus they can be simply combined with “and” operators. The following figure illustrates the use of the UML profile in the case of the Smart House system described above.

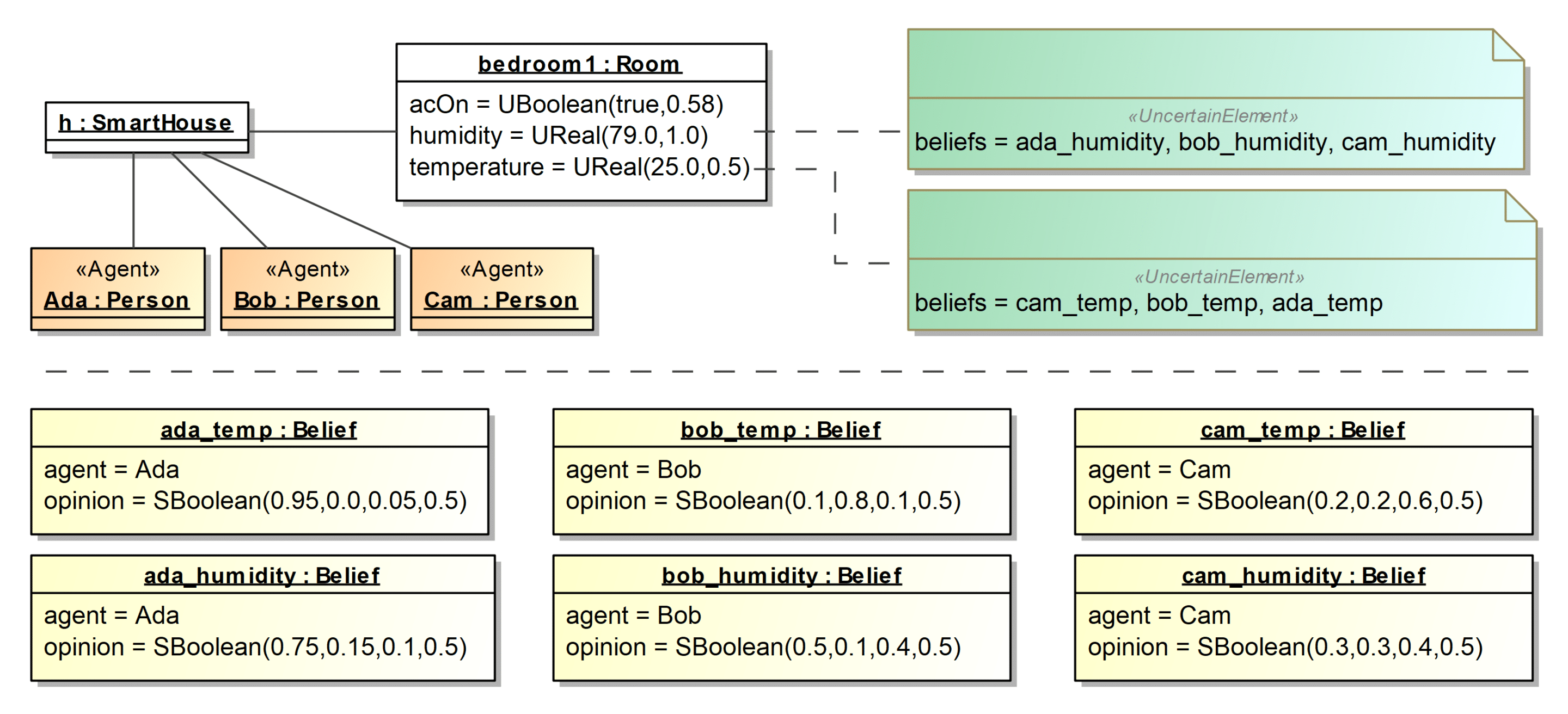
This object model shows a room, bedroom1, annotated with the opinions of three occupants of the house, who hold different opinions on the temperature and humidity values of this object. Namely, Ada is quite confident in her opinions, Bob does not believe in the temperature sensor and partially trust on the humidity readings, and Cam is not sure about any of the sensors. Note that all of them use the same base rate. This is because we are giving an opinion about the correctness of the value. Since we do not have any previous evidence, it is equally probable for it to be wrong or right. The fact that agents hold opinions on the operands of the acOn expression imply a derived opinion on the value of the derived attribute acOn, which is calculated by propagating the opinions through the expression. Although this object model allows agents expressing opinions, we still need to specify how these opinions are propagated through the OCL expressions defined in the model, in particular, in the expression that computes the derived attribute acOn to enable the agents to make decisions.

Belief Fusion Operators

We have extended the type SBoolean with the fusion operators described in [1, 3, 4]. These fusion operators are used to combine the subjective opinions of different belief agents about the same statement, with the goal of producing a single opinion that represents a consensus, or represents the truth more faithfully than each individual opinion. Each fusion operator is designed for a specific purpose and scenario. Depending on the situation, the agents (or the person in charge of merging the opinions) need to decide which fusion operator is the most suitable for each particular case. Let us briefly describe next how they work.

• The Belief Constraint Fusion (BCF) is used when the agents have committed their choices and will not change their minds, at the potential cost of not being able to reach a consensus. Roughly, it computes the overlapping beliefs (the relative Harmony) and the non-overlapping beliefs (the relative Conflict) of the opinions to fuse.
• The Consensus & Compromise Fusion (CCF) preserves the shared beliefs from the sources and transforms conflicting opinions into vague belief. It is suitable for situations in which consensus is sought if it exists, and a vague opinion is acceptable if not. This operator assumes dependence between opinions and it is idempotent with the vacuous opinion as neutral element. It uses a three-steps process: 1) consensus; 2) compromise; 3) merge. The consensus step determines the shared beliefs and disbeliefs between the two opinions. The compromise step redistributes conflicting residual beliefs and disbeliefs to produce the so-called compromise belief. Finally, the merge step distributes that compromise between the shared belief and the uncertainty to compute the resulting opinion. This operator is applicable in situations where (possibly non-expert) agents have dependent opinions about the same fact, such as when they are asked to give their opinions in a survey.
• The Averaging Belief Fusion (ABF) operator assumes that the agents’ opinions are dependent, and the operator is commutative, idempotent, and non-associative. Not having a neutral element means that every opinion, even a vacuous one, influences the fused result. This is the case, for instance, when all agents observe the same situation at the same time, and all opinions should be taken into account. For example, when a jury tries to reach a verdict after having observed the court proceedings. Basically, this operator computes the average of the opinions by weighing the belief of each opinion with the product of the uncertainty of the rest.
• The Weighted Belief Fusion (WBF) operator works as ABF but giving more weight to those opinions with less uncertainty, i.e., the smaller the value of the uncertainty mass, the higher the weight—unlike ABF where all opinions have the same weight even when some of them are very uncertain. This operator has the vacuous opinion as neutral element and, like ABF, it is idempotent.
• The Aleatory and Epistemic Cumulative Belief Fusion operators (ACBF and ECBF, resp.) can be applied when the evidences are independent, i.e., the amount of evidence increases when more agents give their opinion. The Aleatory operator (ACBF) is suitable when giving opinions about a variable governed by a frequentist process, such as flipping a coin. In turn, the ECBF is used for facts whose uncertainty is of epistemic nature. For example, when witnesses express their opinions as to whether they saw the accused at the scene of the crime, which when merged produces an  opinion as to whether the accused was actually there. When the ECBF operator finds contradictory opinions, it increases the uncertainty of the results. Like the ABF, the ACBF operator calculates the mean of the opinions by weighting the belief of each opinion with the product of the uncertainty of the others. However, it modulates this mean by subtracting the product of the uncertainties.

The complete descriptions of the operators’ behavior can be found in [1], with some extensions in [3, 4]. Their full implementation in Java is available in [5]. This implementation is the one used in the UML profile for computing fused opinions.

Different opinions can be fused in various ways, each of which reflects how the specific fusion situation needs to be handled. In general, determining the correct fusion operator best suited for a specific situation is challenging. To address this issue, we have identified a series of characteristics, which may be helpful when determining the operator to use in each case. These can be found in our paper [6].

The motivating example revisited

For illustrative purposes, the following table shows the result of the application of the different fusion operators on the opinions held by the agents of our running example about the value of attribute acOn of object bedroom1.

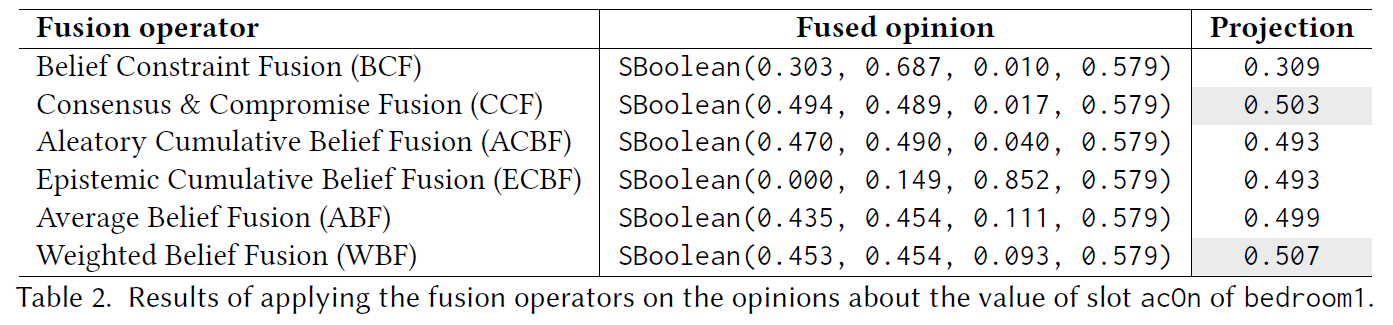
Each row shows the belief fusion operator applied to these values, the resulting opinion, and its projected probability. Depending on the fusion operator used, the merged decision about whether the AC system of that room should be switched on or off changes. Although we have shown in the table the result of all fusion operators for illustrative purposes, note that only CCF and WBF apply to this particular situation. Since both CCF and WBF present a small degree of uncertainty and have a projection above 0.5, which means that the AC system should be switched on (merging the disparate opinions of Ada, Bob and Cam).

Methodology – Guidelines to use our approach

Although any methodology could be used to realize our approach, we devised it within a collaborative and iterative process, with the following steps in mind.

1. Each agent involved in the design of a domain starts instantiating the domain model. This instance model that represents the system under study might not be the same for all agents: each agent may have independently developed a different model according to the information they have, their sources, and their individual perceptions.
2. Using our Belief profile, agents annotate those instances and links for which they are uncertain about their existence as well as those attributes for which they are uncertain about their actual values. Annotations are expressed in terms of beliefs. Model elements with no assigned beliefs are assumed to be dogmatic trues, i.e, SBoolean(1,0,0,1).
3. The belief uncertainty information is automatically propagated to the derived properties and operations of the model.
4. Once the agents have their individual instantiations of the domain model enriched with their subjective opinions, they can decide to merge these object models. This process builds a model with the union of all elements and links, and their annotations. Unless otherwise agreed by the agents, by convention, those elements present in the object model of one agent but not in the object model of others will appear in the merged object model, but they will be stereotyped as «UncertainElement» and will have one opinion with value SBoolean(0,1,0,0) (i.e., the dogmatic false) by each one of agents that did not have it in their individual instance.
5. After observing each other’s opinions in the merged model, the belief agents can reconsider their opinions. This can lead to a repetition of step 2. of this process.
6. When the combined object model with the aggregated opinions of all the agents is ready, the individual opinions can be merged. To do this, they need to select the appropriate fusion operator(s) that can be applied for each particular scenario.
7. Then, decisions can be made depending on the resulting fused opinions, and their degree of uncertainty (see the considerations below about the cost of being wrong).
8. Finally, in light of the resulting decisions, the belief agents can iteratively reconsider their individual opinions or the fusion operator to be used, and the process can start again until a consensus is reached.

A particular scenario occurs when there are no different independent models, one from each agent, but the model is the same for all, and the agents add their opinions on this common model. In such a case, only steps 2., 3., 5., 6., 7. and 8. apply.

Tool support

We have implemented our Belief profile in MagicDraw. Once an instance model is developed, stereotyped, and its model elements are assigned opinions using the profile, the user may want to fuse opinions. For this, we have created a MagicDraw plugin.

The following figure shows a screenshot of MagicDraw including our profile and plugin.

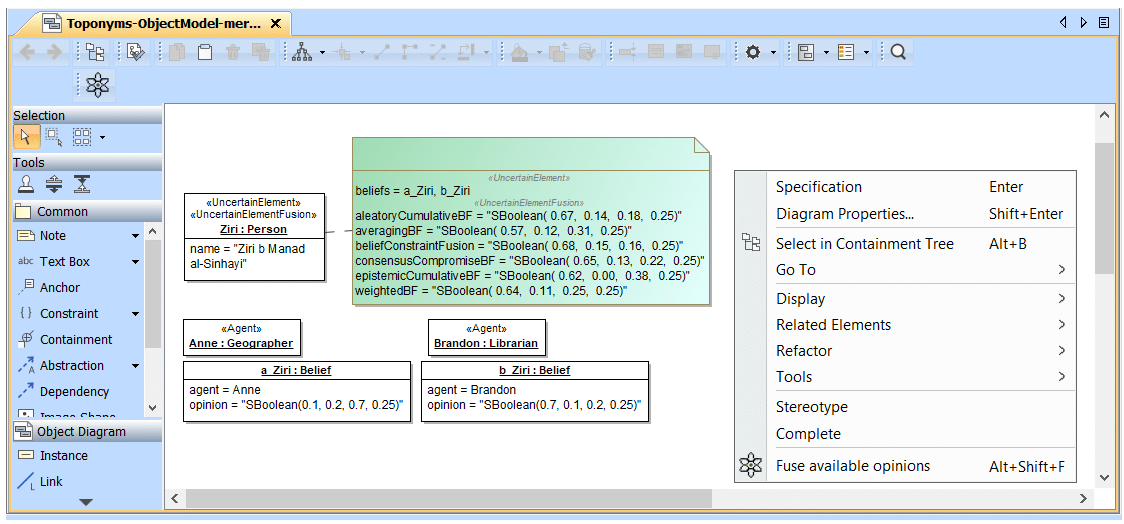
From the point of view of the final user, one only has to either click on the fusion button on the menu or right-click and select the option Fuse available opinions, then the result of the fusion operators shows in the model — see the tag values in the note in green that are placed under the «UncertainElementFusion» stereotype. Let us remind the reader that, since these tags have been defined in the profile, they extend the instance model but do not modify it.

Internally, our plugin traverses the object models and, for each element that is stereotyped as «UncertainElementFusion», it collects all available opinions, performs the required validity checks (e.g., opinions must be from different agents, base rates must be equal for some of the operators, etc.) and fuses them. For the fusion, we have developed a Java library that implements all the fusion operators described above. The plugin calls the Java library API every time that opinions need to be fused.

Evaluation

In order to evaluate the feasibility, applicability and usability of our proposal, we have developed several application scenarios and we have performed an empirical study with users. For details about how our evaluation was carried out, we refer the reader to our paper [6].

As a summary of the results and lessons learned, we can confirm that, in the application scenarios, our profile was capable of capturing the beliefs of different stakeholders and the fusion operators provided a way to merge these opinions in order to make informed decisions, demonstrating the feasibility of our contribution. In the empirical study, most of the participants found our proposal useful, expressive and usable. We observed how the learning curve is steeper at the beginning, which is reflected in some incorrect answers to the initial questions. However, as the experiment progressed and participants became familiar with all the concepts of our proposal, they were able to use it faster and correctly. The participants also expressed that the selection of the most suitable fusion operator was the most difficult task. However, the results show that all of them were able to succeed in this task. We believe that, with some training, good documentation and/or examples, this aspect does not hinder the application of our proposal. Nevertheless, we plan to investigate how we can better assist users in this step in the future. The fact that participants explicitly saw the opinions of other members before and during their consensus-building discussions made them realize that their opinions could be refined. This shows that our iterative methodology was faithfully put in practice.

Conclusions

Belief uncertainty is a type of epistemic uncertainty in which a belief agent is uncertain about the truth of a statement. In this work [6], we have presented our approach and methodology to capture, represent and operate with belief uncertainty in domain models. In order to achieve our goal, we use Subjective Logic to capture the subjective opinions of the agents involved in the modeling process of a domain, including their degree of belief, disbelief and uncertainty. We have created a UML profile to represent the agents’ beliefs in instance models in such a way that the domain model is extended but not altered. In addition, we have addressed the challenge of combining the opinions from different belief agents on the same model elements and have provided a mechanism to operate with these opinions. This mechanism supports decision-making by enabling agents to arrive at global, informed decisions by using optimal strategies to merge individual opinions.

This is of utmost relevance for decision makers, since decisions based on probabilities with low confidence could lead to exorbitant mistakes. The validation performed was aimed at answering the two research questions we initially posed: how can users capture and explicitly represent their opinions about the instances of domain models (RQ1), and then reason about these opinions to reach informed decisions (RQ2). First, we showed how opinions could be expressed in several exemplar applications from different domains, illustrating different applications of our proposal. Next, the experiment conducted has shown how different sets of users could effectively use our UML profile to express their opinions about instance models, and then use the fusion operators to help them reach conclusions successfully, i.e., users were able to successfully apply our methodology and our tool supported the entire process. As part of our future work, we plan to empirically evaluate both the usability and usefulness of our approach with users in real contexts.

Moreover, we are aware of the UML/OCL benefits to represent and operate with beliefs, but we also understand their drawbacks. Depending on the final user profile, their background and competences, UML may not be the most appropriate base language for our approach. In this sense, we would like to explore different notations such as tailored DSLs, easier to adapt to the vocabulary and technical knowledge of specific user communities.

Finally, there are different reasons for an agent to be uncertain about a particular statement (conflicting sources, second-hand opinions, incomplete information, …). We are interested in defining a taxonomy for these reasons, in order to improve the annotation of a model. We believe this information can be useful when choosing a particular belief fusion operator. This could also be very useful when extending our approach to other types of models, such as sequence diagrams and

References

[1] Audun Jøsang. 2016. Subjective Logic – A Formalism for Reasoning Under Uncertainty. Springer. https://doi.org/10.1007/978-3-319-42337-1

[2] Manuel F. Bertoa, Lola Burgueño, Nathalie Moreno, and Antonio Vallecillo. 2020. Incorporating measurement uncertainty into OCL/UML primitive datatypes. Softw. Syst. Model. 19, 5 (2020), 1163–1189. https://doi.org/10.1007/s10270-019-00741-0

[3] Audun Jøsang, Dongxia Wang, and Jie Zhang. 2017. Multi-source fusion in subjective logic. In Proc. of FUSION’17. IEEE, 1–8. https://doi.org/10.23919/ICIF.2017.8009820

[4] Rens Wouter van der Heijden, Henning Kopp, and Frank Kargl. 2018. Multi-Source Fusion Operations in Subjective Logic. In Proc. of FUSION’18. IEEE, 1990–1997. https://doi.org/10.23919/ICIF.2018.8455615

[5] Lola Burgueño, Paula Muñoz, Robert Clariso, Jordi Cabot, Sebastien Gerard, and Antonio Vallecillo. 2021. Belief Fusion Plugin – Git Repository. https://github.com/atenearesearchgroup/belief-fusion-plugin.

[6] Lola Burgueño, Paula Muñoz, Robert Clarisó, Jordi Cabot, Sébastien Gérard, Antonio Vallecillo. Dealing with belief uncertainty in domain models. ACM Transactions on Software Engineering and Methodology. 2022.