Defining appropriate integrity constraints (ICs) for the domain model of a software system is a complex and error-prone task. Both over-constraining or under-constraining the data are undesirable.
As a solution, we propose a systematic approach to explore the most suitable constraints for a software system. The inputs of this approach are an initial tentative set of constraints described in OCL (Object Constraint Language) plus a sample information base which is incorrectly forbidden (allowed) by them. Then, this method generates candidate weaker (stronger) versions of the ICs by mutating them in a structured way. Modelers can then replace the original defective set with the alternative versions to improve the quality of the domain model.
Our proposal will be part of the Quatic’18 conference (11th International Conference on the Quality of Information and Communications Technology). You can download the full pdf for the Fixing defects in integrity constraints via constraint mutation paper or keep reading to get a better understanding on how our method works.
Contents
On the subtle art of writing integrity constraints and business rules
The design of the domain model of a software system is a complex process. A key activity within this process is the definition of the integrity constraints (IC) that restrict the information base (IB), the set of objects and links that can instantiate the model, to take into account the well-formedness rules of the particular domain and the business rules. These constraints can be described, for instance, as invariants written in the Object Constraint Language3 (OCL).
ICs are in charge of making sure that the information base is both valid and complete [23] at all times. Therefore, the correctness of the ICs plays a major role in the quality of the overall software system. Indeed, incorrect ICs may cause a valid information base to be labeled as invalid, or vice-versa. Faulty ICs may arise due to a modeler oversight during the initial blank-slate design of a domain model. They may also occur during an iterative or example-driven design, where tentative designs are refined as more information is gained through examples [3]. Moreover, they may also be caused by the evolution of the software system, due to changes in the domain or the business rules.
Some errors in the definition of the ICs can be fixed by looking at the constraint themselves and/or their interrelationships, e.g. syntactical or consistency errors [13]. A more complex scenario arises when the constraint is apparently cor- rect (or at least satisfiable) but fails to faithfully represent the modeler’s intent. In particular, it may happen that the IC is almost correct but is too restrictive or too lax, in the sense that it forbids (allows) valid (invalid) configurations of the information base. These are the kind of faulty constraints we focus on.
Fixing an incorrect IC is an error-prone process in itself, as modelers may accidentally introduce new errors during the fix. For instance, it may be relevant to ensure that fixing an invariant which is too restrictive makes it laxer, without forbidding new configurations unintendedly. Thus, it is desirable to provide methods and tools that can support modelers in this process.
In this sense, this paper proposes a method to fix integrity constraints that are found to be too restrictive or too lax. The method requires two inputs: the current candidate IC and the information base where this IC has an undesired behavior. We will assume that the IC is expressed as an OCL invariant, but the process can be easily generalized to other similar declarative constraint languages. Then, the method explores alternative ICs by mutating the original constraint. A systematic procedure is used to generate mutants, which ensures that generated ICs are stronger than the original (or weaker, depending on the goal) and that the strongest (weakest) among them can be selected. In this way, it differs from other works that perform OCL mutation, e.g. for testing purposes.
Related work on constraint mutation
Veriftcation and validation of integrity constraints. Many works check the consistency of ICs written in OCL [13], e.g. among others the USE en- vironment [12, 19]. If they are consistent, a sample valid information base is computed. Otherwise, some methods compute a (minimal) subset of inconsis- tent constraints, e.g. using unsatisfiable cores [26] or Max-SAT solvers [28]. In order to gain a better understanding of the model, it is also possible to identify which parts of a valid information base are “mandatory” and which parts can be modified without violating the ICs [21]. In contrast, rather than detecting and understanding errors, our method aims at fixing incorrect constraints.
Integrity constraint mining. Several works have considered the automatic in- ference of the integrity constraints of a software system [9,11]. These approaches start from a collection of example and counterexample IBs. Initial candidate invariants are generated by using patterns or templates that represent frequent or likely invariants [9, 11]. From these initial candidates, new invariants can be discovered through search, e.g. using genetic algorithms [11].
These works follow the inductive learning paradigm: infer general rules from a limited set of observations. They are related to our approach as (a) they generate candidate invariants for a software system and (b) one of them [11] uses mutation to generate new candidates. However, our approach differs from these methods in several ways:
- It is not restricted to specific constraints
- It can take advantage of existing knowledge about the integrity
- Its goal is more precise: fixing over- or under-constrained integrity constraints, rather than inferring the entire set of integrity
- It certifies that the fixed invariants are stronger (weaker) than the
- It only requires a single information base to operate, rather than a (large) collection of annotated examples and Generating or label- ing those examples may be time-consuming and error prone.
In the database domain, [10] infers ICs from the tuples in a database. Only a restricted subset of relational algebra constraints is supported: quantified formulas, which are a central part of OCL, are not allowed. Another strategy is considering tuples that violate ICs as exceptions that must be handled separately, rather than errors that need to be fixed. Fixes of the form “if exception then special-case else integrity-constraint” are studied in [5]. Finally, [22] considers the problem of fixing integrity constraints when a deviation, e.g. an inconsis- tent instance, is found. However, it requires a human expert to provide a list of candidate fixes, while this paper proposes these fixes automatically.
Domain knowledge acquisition. Several works aim at helping the modeler capture prior domain knowledge in the form of integrity constraints. For example,
- proposes an interactive dialog with the modeler, through the use of examples, to infer simple integrity constraints, e.g. cardinalities or key constraints. [16] considers an iterative process that generates candidate databases according to different integrity constraints to help the modeler select the most suitable
Mutation testing. Mutation testing [18] is a white-box testing technique which studies the correctness of a piece of software by introducing small changes called mutations. The ability of a test case or test suite to detect mutants can be used as an indicator of its coverage and quality.
In the context of OCL, several catalogs of mutation operators for mutation testing of UML class diagrams or sequence diagrams have been defined [1,15,27]. While the operators proposed in the literature are similar in spirit to the ones discussed in this paper, there are two key differences with our approach:
- The goal of the analysis (finding defects through testing versus finding can- didate fixes for those defects)
- The way mutation operators are applied (randomly versus systematically)
Automatic software repair. Automatic program repair, e.g. [20, 25], aims to compute fixes for errors in imperative programs without human interven- tion. Candidate fixes can be generated using patterns, genetic algorithms or SMT solvers. However, even methods that specifically target errors in condi- tional statements [29] are not suitable in this context: a test suite including positive examples is required as input (rather than a single negative example) and the correctness of the fix is only assured with respect to the test suite (rather than assuring that the fix is a weaker or stronger constraint in general).
In the database domain, [14] targets incorrect SELECT statements in ABAP programs and uses machine learning to suggest fixes. Meanwhile, other works fo- cus on scenarios with correct integrity constraints and invalid information bases. Thus, they are concerned with problems such as database repair [24] (perform minimal updates to the information base to make it valid) or consistent query answering [4] (ensure that answers to queries do not include inconsistent data). Finally, [8] proposes a method that, given an invalid information base, decides whether it is more cost-effective to repair the information base or the ICs. However, this method only supports simple ICs (primary and foreign key constraints) and one type of repair (adding attributes to the key).
Other works. The evolution of a domain model can introduce changes that affect the syntactic correctness of ICs. [17] provides a set of tools to refactor ICs after those changes, but simply intends to preserve their syntactic correctness.
Our constraint fixing method
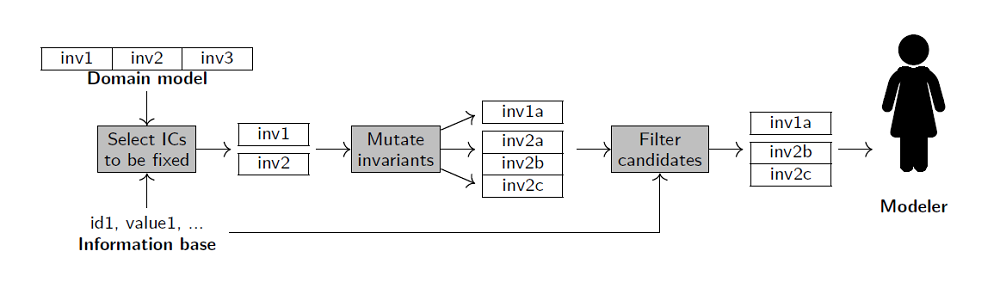
In this section, we present our approach for fixing OCL invariants that are flagged by the modeler due to showing an undesired behaviour when validating them over sample sets of IBs.
Section 3.1 presents an overview of the approach and introduces a running example. Section 3.2 explains how the invariants that need to be fixed are identified. Then, Section 3.3 describes how they are transformed in order to generate candidate fixes. Finally, Section 3.4 illustrates how the candidate fixes can be pruned and filtered before being presented to the modeler.
1. Overview
Our method can operate in two different modes: weakening, when the existing integrity constraints are too restrictive; and strengthtening, when they are too lax. In the following, we will use the term mutate to refer to the application of the method, either in weakening or strengthening mode.
In both operation modes, only two inputs are required:
- A domain model of the software system which includes integrity constraints defined as OCL
- An IB where the modeler detects that the OCL invariants do not yield the desired valid/invalid
The output of this method will be a list of candidate ICs that should replace some of the existing ICs that are considered defective. The modeler will need to inspect these candidates and select the ones which seem most suitable.
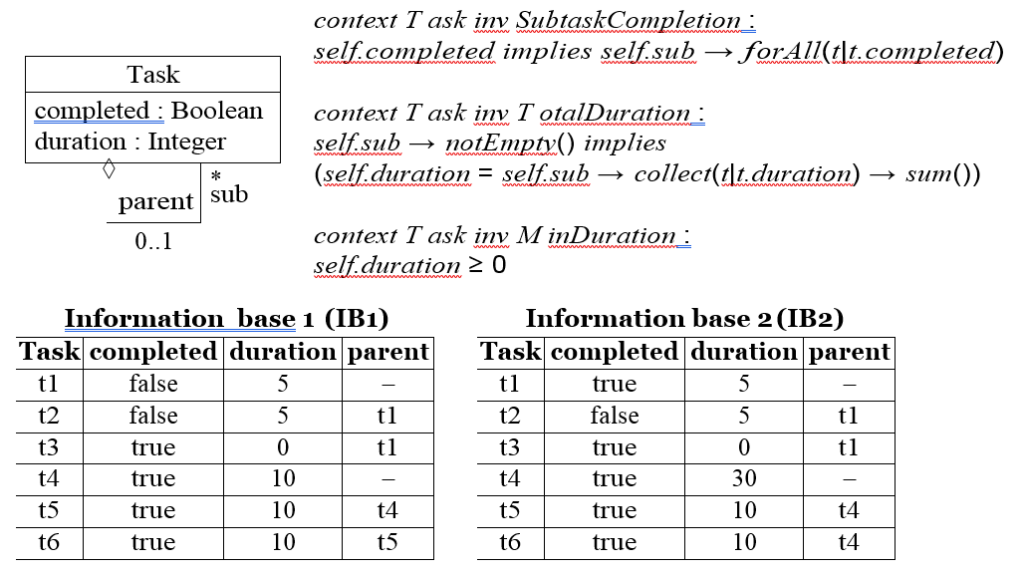
Example 1. Let us consider a simple domain model for task management, where each task may be composed of subtasks. Each task has a duration and may be flagged as “completed”.
Figure 1 shows the integrity constraints for this domain model and two potential information bases (IB1 and IB2). While IB1 is valid according to the integrity constraints, IB2 is invalid: task t1 violates invariant SubtaskCompletion (t1 is completed even though its subtask t2 is not) while task t4 violates invariant TotalDuration (task t4 has a duration which is different from the total duration of its subtasks t5 and t6). Assuming IB2 is considered valid by the modeler, it means that the ICs are incorrectly defined because they do not properly represent the requirements of the domain and therefore should be repaired.
When fixing the ICs to accept IB2, it is important to make sure that the fix does not inadvertently forbid valid information bases like IB1. That is, we need to make sure that the fix is less restrictive than the existing invariant. We will illustrate this process called weakening as our running example.
2. Selecting the invariants of interest
The method operates on the abstract syntax tree (AST) of the OCL invariants, which is generated by any OCL tool such as EMF as part of the parsing process.
First, we need to identify which invariants need to be mutated. This process will be different for each operation mode:
- In the case of weakening, the ICs are too restrictive, so some OCL invariants will be violated by the valid These will be our invariants of interest.
- When we apply strengthening, ICs are too lax so none of them will be violated by the invalid Selecting ICs can be done in two different ways:
- Suggest potential changes for each invariant and let the modeler choose the most suitable change; or
- Ask the modeler to select which invariant should be responsible for detecting this violation.
The first strategy reduces the effort required from the modeler before the application of the method, while the second reduces the number of alternatives that will be presented to the modeler during the analysis.
Example 2. In the running example, only invariants SubtaskCompletion and TotalDuration need to be weakened. Thus, invariant MinDuration can be ignored in our analysis.
2. Mutating the invariants of interest
Given a list of OCL invariants that have to be mutated, the next step of this method generates a list of candidate fixes for each invariant. In this section, we will focus on how the fixes are generated, while Section 3.4 will focus on the overall search strategy: which fixes should be computed, in which order and which ones should be shown to the modeler.
Our mutation will operate on the AST of the OCL constraint. We will consider two types of expressions in our analysis: boolean expressions and collection expressions. For boolean expressions, we will consider two types of mutation operators: weaken, computing weaker versions of the original expression; and strengthen, computing stronger versions of the original expression. Similarly, for collections there are two types of mutation operators: hull, computing a superset of the original collection; and kernel, computing a subset of the original collection. The mutation operator to be used will depend on our overall goal.
Formal definitions. The OCL notation uses a four-valued logic which includes “true”, “false” and two special values: null and invalid. The null value indicates non-existent data, e.g. accessing an attribute with multiplicity 0..1. Meanwhile, the invalid value corresponds to errors in the evaluation of the expression, e.g. a division by zero or invoking an operation with an invalid argument. As a general rule, boolean operators evaluate to invalid if any operand is invalid and to null if any operand is null (and no other operand is invalid). However, boolean operators use a short-circuit semantics as in the C language, e.g. if the first operand of an “and” expression is false, the result is false regardless of the second operand. That is, while “true and null” is null, “false and null” is false due to short-circuit.
Definition 1(Weaken and strengthen). Given a boolean OCL expression e, a weakening (strengthening) of e, denoted as e− (e+), is another OCL boolean expression such that in any IB, the value obtained by evaluating e− (e+) is related to the value obtained by evaluating e in the following way:
| original (e) | weakening (e−) | strengthening (e+) |
| true | true | {true, null, invalid, false} |
| null | {true, null, invalid} | {null, invalid, false} |
| invalid | {true, null, invalid} | {null, invalid, false} |
| false | {true, null, invalid, false} | false |
Example 3. In Boolean logic, A or B is weaker than A and B. Our definition of weaken and strengthen allows us to extend this notion to 4-valued logic. For instance, if A is false and B is invalid, then A or B = invalid and A and B = false.
Definition 2(Hull and kernel). Given an OCL expression e of type Set(T ) or Bag(T ), the hull (kernel) of e, denoted as e↑ (e↓), is another OCL expression of the same type such that in any information base:
- Hull: e is included in e↑, i.e. e ⊆ e↑, and all the new elements conform to type T , i.e. e↑ → f orAll(x|x.oclIsKindOf (T )).
- Kernel: e↓ is included in e, i.e. e↓ ⊆ e.
Mutation process. The process will start at the root of the IC that needs to be mutated, as identified in the previous phase (see Section 3.2). For each node n in the AST, several candidate fixes may be available, and this typically requires recursively generating mutants (weaken, strengthen, hull or kernel) for subexpressions of n. For instance, weakening the expression not X will require strengthen- ing X, while strengthening a forAll quantifier like Col forAll(x Exp) can be achieved by strengthening Exp, by computing the hull of Col or both.
Due to space constraints, in the paper we will only discuss the implementation of the mutation operators weaken and hull. The mutation operators strengthen and kernel have an analogous implementation. For example, strengthening an “or” operator is similar to weakening an “and” operator.
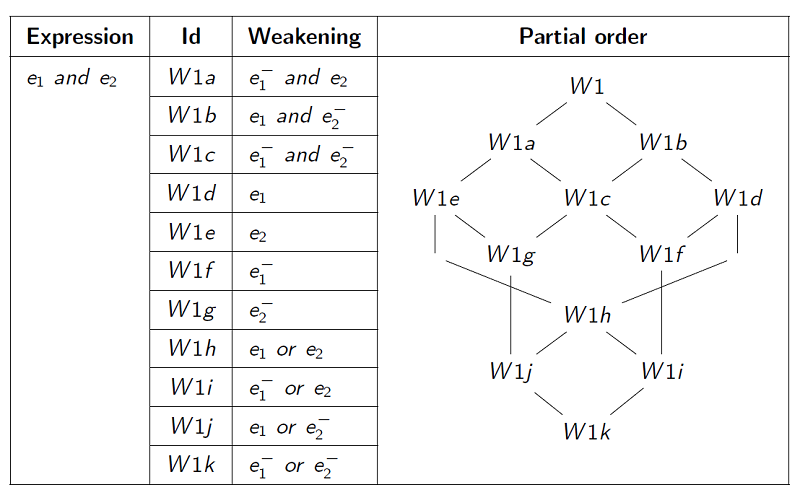
With respect to weakenings, we need to define the semantics of weakening for the different types of OCL constructs computing a boolean value: logic operators (Table 1), relational operators (Table 2), quantifiers (Table 4) and other operations (Table 3). Intuitively, weakening may modify the operator and it may require to mutate the subexpressions, either by performing a weakening, strengthening, hull or kernel. Note that these Tables are not exhaustive: there is an infinite number of potential mutations for a given expression. For instance, given a Boolean expression Cond it is always possible to strengthen it by adding a new condition Cond and newCond, and to weaken it adding a disjunction. Given the unboundedness of such strategies, we do not consider this type of mutations. Meanwhile, Table 5 defines the mutation operators for computing the hull of OCL collection expressions. Similarly to how it is done for weakening, computing the hull may require modifying the operator or mutating the subexpressions. In these tables, there is a partial order among the mutants of an OCL expression, i.e. some may be stronger or weaker than others. For a given expression e, weakenings (strengthenings) define a lattice. This lattice is used to select an order to generate mutants and to prune the list of candidate fixes.
We show here just one of these tables (with the corresponding partial order). Refer to the full paper text for the complete details
Example 4. Figure 2 shows the weakenings for the two incorrect invariants in our running example that would be presented to the modeler. For TotalDuration, we replace the equality by greater-or-equal (operator W1a from Table 2). Intuitively, it means that a task takes at least the duration of its subtasks, but it may also take longer. For SubtaskCompletion, we replace “forAll” quantifier by “exists”. That is, rather than requiring all subtasks to be completed before completing a task, this fix only requires that at least one of them is completed. Notice that we also check for tasks with no subtasks, otherwise, the fix would not be a correct weakening: it would evaluate to false instead of true in these tasks. The computation of this weakening proceeds as follows. First, in the top “implies” expression we weaken the rightmost subexpression (pattern W4b, Table 1). This expressions is a quantifier “forAll”, which can be weakened by replacing it with an existential quantifier (pattern W1d, Table 4).
4. Selecting the candidate ftxes
Once a candidate fix to an OCL invariant is generated, it can be automatically checked by evaluating it on the IB. The criteria to decide whether the fix is successful depends on the operation mode:
- Weakening : Evaluation can be limited to the objects where the original invariant evaluates to false. The fix is successful if the fixed invariant now evaluates to true in all of these objects.
- Strengthening : The fixed invariant must be evaluated over the entire IB. The fix is successful if it evaluates to false in at least one object.
However, not all successful candidate fixes will be equally relevant. Given a weakened (strengthened) condition that is a successful fix for an invariant, any weaker (stronger) condition will also be a successful fix. For instance, if an invariant A and B needs to be weakened and A is a successful fix, then A or B will also be a successful fix. Thus, it is sufficient to report the strongest (weakest) among all potential weakenings (strengthenings). The partial orders defined by mutants for each type of OCL expression can help us detect when one expression is weaker or stronger than another one. However, notice that, given that the lattice is a partial order, some fixes are neither stronger nor weaker than other fixes. After filtering weaker (stronger) fixes, the remaining candidate fixes should be presented to the modeler so that she can choose among them.
Furthermore, information about stronger and weaker mutants can guide the search for candidate fixes in order to avoid generating a fix if a stronger one (for weakenings) or a weaker one (for strengthenings) has already been found to be successful. The procedure would work by performing a breadth-first traversal of the partial order starting from the top (weakening) o bottom (strengthening). At each node, we generate the proposed fix (or fixes, as they may require mutating subexpressions). If a fix is successful, then we can mark the descendants of this node to avoid visiting them.
Conclusions
In this paper, we have presented a method for discovering fixes for over(under)- constrained integrity constraints modeled as OCL invariants. The method relies on the mutation of OCL constraints, a technique which is typically employed for testing purposes. Instead of applying mutations randomly in order to introduce faults in the initial set of constraints, we define a procedure to explore mutants systematically in a way that allows selecting the strongest (weakest) among them while still properly allowing (restricting) the information base given as input.
As future work, we plan to extend our method to transition constraints described using operation contracts, which may suffer from the same kind of faults. Furthermore, our proposed mutations can be used in model verification (in combination with SAT solvers to fix inconsistencies among a set of constraints by mutating some of them until the model becomes satisfiable) and to guide mutation testing, i.e. generating mutants whose constraints are guaranteed to be more restrictive or more lax depending on the needs, which can be useful in certain testing scenarios. Finally, we will also consider heuristics to organize potential candidate fixes in order to reduce the amount of work required by the modeler during revisions. We plan to integrate these strategies as extensions to our EMFtoCSP tool [6].
References
1.B. Aichernig and P. Pari Salas. Test Case Generation by OCL Mutation and Constraint Solving. In QSIC’05, pages 64–71. IEEE, 2005.
2.M. Albrecht, E. Buchholz, A. D usterh oft, and B. Thalheim. An informal and efficient approach for obtaining semantic constraints using sample data and natural language processing. In Semantics in databases, 1998.
3.K. Bąk, D. Zayan, K. Czarnecki, M. Antkiewicz, Z. Diskin, A. Wąsowski, and Rayside. Example-driven modeling: Model = abstractions + examples. In ICSE’13, pages 1273–1276. IEEE Press, 2013.
4.L. Bertossi and Leopoldo. Consistent query answering in databases. ACM SIG- MOD Record, 35(2):68, 6 2006.
5.A. Borgida, T. Mitchell, and K. E. Williamson. Learning Improved Integrity Con- straints and Schemas From Exceptions in Data and Knowledge Bases. In On Knowledge Base Management Systems, pages 259–286. Springer, 1986.
6.J. Cabot, R. Clarisó, and D. Riera. On the verification of UML/OCL class diagrams using constraint programming. Journal of Systems and Software, 93:1–23, 7 2014.
7.J. J. Cadavid, B. Combemale, and B. Baudry. An analysis of metamodeling practices for MOF and OCL. Computer Languages, Systems & Structures, 41:42–65, 2015.
8.F. Chiang and R. J. Miller. A unified model for data and constraint repair. In ICDE’2011, pages 446–457. IEEE Computer Society, 2011.
9.D.-H. Dang and J. Cabot. On Automating Inference of OCL Constraints from Counterexamples and Examples. In KSE’14, pages 219–231. Springer, 2014.
10.J. P. Delgrande. Formal limits on the automatic generation and maintenance of integrity constraints. In PODS’87, pages 190–196. ACM Press, 1987.
11.M. Faunes, J. Cadavid, B. Baudry, H. Sahraoui, and B. Combemale. Automati- cally Searching for Metamodel Well-Formedness Rules in Examples and Counter- Examples. In MODELS’13, pages 187–202. Springer, Berlin, Heidelberg, 2013.
12.M. Gogolla, F. Hilken, and K.-H. Doan. Achieving model quality through model validation, verification and exploration. Computer Languages, Systems & Struc- tures, 2017.
13.C. A. González and J. Cabot. Formal verification of static software models in MDE: A systematic review. Information and Software Technology, 56(8):821–838, 8 2014.
14.D. Gopinath, S. Khurshid, D. Saha, and S. Chandra. Data-guided repair of selection statements. In ICSE’14, pages 243–253. ACM Press, 2014.
15.M. F. Granda, N. Condori-Fernández, T. E. J. Vos, and O. Pastor. Mutation Operators for UML Class Diagrams. In CAISE’16, pages 325–341. Springer, 2016.
16.S. Hartmann, S. Link, and T. Trinh. Constraint acquisition for Entity-Relationship models. Data & Knowledge Engineering, 68(10):1128–1155, 10 2009.
17.K. Hassam, S. Sadou, V. L. Gloahec, and R. Fleurquin. Assistance System for OCL Constraints Adaptation during Metamodel Evolution. In CSMR’11, pages 151–160. IEEE, 3 2011.
18.Y. Jia and M. Harman. An Analysis and Survey of the Development of Mutation Testing. IEEE Transactions on Software Engineering, 37(5):649–678, 9 2011.
19.M. Kuhlmann, L. Hamann, and M. Gogolla. Extensive validation of OCL models by integrating SAT solving into USE. In TOOLS’2011, pages 290–306, 2011.
20.C. Le Goues, S. Forrest, and W. Weimer. Current challenges in automatic software repair. Software Quality Journal, 21(3):421–443, 9 2013.
21.T. Nelson, N. Danas, D. J. Dougherty, and S. Krishnamurthi. The power of “why” and “why not”: enriching scenario exploration with provenance. In ESEC/FSE’2017, pages 106–116. ACM, 2017.
22.E. D. Nitto and L. Tanca. Dealing with deviations in DBMSs: An approach to revise consistency constraints. In FMLDO’96, pages 11–24, 1996.
23.A. Olivé. Conceptual Modeling of Information Systems. Springer Berlin Heidelberg, Berlin, Heidelberg, 2007.
24. Oriol, E. Teniente, and A. Computing repairs for constraint violations in UML/OCL conceptual schemas. Data & Knowledge Engineering, 99:39–58, 2015.
25. Pei, C. A. Furia, Nordio, Y. Wei, B. Meyer, and A. Zeller. Automated Fixing of Programs with Contracts. IEEE Transactions on Software Engineering, 40(5):427–449, 5 2014.
26.E. Torlak, F. S. Chang, and D. Jackson. Finding minimal unsatisfiable cores of declarative specifications. In FM’2008, volume 5014 of Lecture Notes in Computer Science, pages 326–341. Springer, 2008.
27.S. Weissleder and B.-H. Schlingloff. Quality of Automatically Generated Test Cases based on OCL Expressions. In ICST’2008, pages 517–520. IEEE, 4 2008.
28.H. Wu. MaxUSE: A tool for finding achievable constraints and conflicts for in- consistent UML class diagrams. In IFM’2017, volume 10510 of Lecture Notes in Computer Science, pages 348–356. Springer, 2017.
29.J. Xuan, M. Martinez, F. Demarco, M. Clement, S. R. L. Marcote, T. Durieux, L. Berre, and M. Monperrus. Nopol: Automatic repair of conditional statement bugs in Java programs. IEEE Trans. Software Eng., 43(1):34–55, 2017.
Robert Clarisó is an associate professor at the Open University of Catalonia (UOC). His research interests consist in the use of formal methods in software engineering and the development of tools and environments for e-learning.


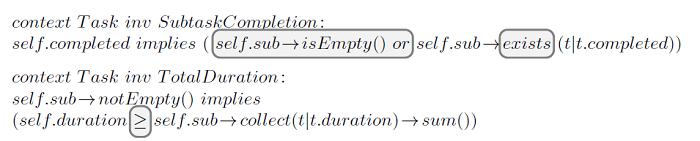


Recent Comments