As part of the MELO workshop (Workshop on Model-Driven Engineering, Logic and Optimization), Martin Gogolla gave a keynote on the need for OCL benchmarks that help us to evaluate and compare OCL tools.
This talk followed up on a previous work we did together (see Initiating a benchmark for UML and OCL analysis tools) so after the workshop we decided to sit down together and work on an updated version on this proposal to be part of the workshop proceedings:
You can also get the free pdf version of the text or just keep reading here:
Contents
Abstract
UML and OCL are frequently employed languages in model-based engineering. OCL is supported by a variety of design and analysis tools having different scopes, aims and technological corner stones. The spectrum ranges from treating issues concerning formal proof techniques to testing approaches, from validation to verification, and from logic programming and rewriting to SAT- based technology.
This paper presents steps towards a well-founded benchmark for assessing UML and OCL validation and verification techniques. It puts forward a set of UML and OCL models together with particular questions centered around OCL and the notions consistency, independence, consequences, and reachability. Further- more aspects of integer arithmetic and aggregations functions (in the spirit of SQL functions as COUNT or SUM) are discussed. The claim of the paper is not to present a complete benchmark. It is intended to continue the development of further UML and OCL models and accompanying questions within the modeling community having the aim to obtain an overall accepted benchmark.
Introduction
Model-driven engineering (MDE) as a paradigm for software development is gaining more and more importance. Models and model transformations are central notions in modeling languages like UML, SysML, or EMF and transformation languages like QVT or ATL. In these approaches, the Object Constraint Language (OCL) can be em- ployed for expressing constraints and operations and therefore OCL plays a central role in MDE.
A variety of OCL tools and verification/validation/testing techniques around OCL are currently available (e.g. [16], [22], [10], [14], [6, 15], [4], [2], [1], [19], [3], [11], [23], [21], [17], [8], [9]) but it is an open issue how to compare such tools and sup- port developers in choosing the OCL tool most appropriate for their project. In many other areas of computer science this comparison is performed by evaluating the tools over a set of standardized benchmark able to provide a somewhat fair comparison envi- ronment. Unfortunately, such benchmarks are largely missing for UML and practically inexistent for OCL.
In this sense, this paper continues the initial proposal of a set of UML/OCL bench- marks [13] and puts forward a couple of complementary benchmark models and a few ideas to encourage the community to have an active participation in this benchmark creation and acceptance process. The two new scenarios focus on integer arithmetic (area that has a significant effect on the tool efficiency depending on the underlying formalism used in the reasoning tasks) and large models with heavy use of aggregated functions, a topic for which the OCL language itself has limited coverage [7].
The structure of the rest of this paper is as follows. The next section gives a short introduction to OCL. Section 3 reviews the initial set of models in our benchmark. Section 4 puts forward additional benchmark models while Section 5 discusses possible actions to take to further extend the benchmark. The paper is finished in Sect. 6 with concluding remarks.
OCL in a nutshell
The Object Constrains Language (OCL) is a textual, descriptive expression language. OCL is side effect free and is mainly used for phrasing constraints and queries in object- oriented models. Most OCL expressions rely on a class model which is expressed in a graphical modeling language like UML, MOF or EMF. The central concepts in OCL are objects, object navigation, collections, collection operations and boolean-valued ex- pressions, i.e., formulas. Let us consider these concepts in connection with the object diagram in Fig. 1 which belongs to the class diagram in Fig. 2. This class diagram captures part of the submission and reviewing process of conference papers. The class diagram defines classes with attributes (and operations, not used in this example) and associations with roles and multiplicities which restrict the number of possible connected objects.
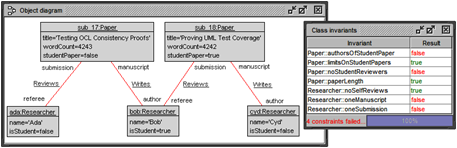
Fig. 1. Object Diagram for WR
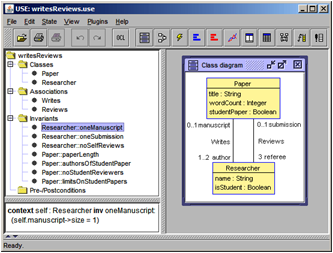
Fig. 2. Class Diagram for WR
Objects: An OCL expression will often begin with an object literal or an object vari- able. For the system state represented in the object diagram, one can use the objects ada,bob,cyd of type Researcher and sub_17,sub_18 of type Paper. Furthermore variables like p:Paper and r:Researcher can be employed.
Object navigation: Object navigation is realized by using role names from associations (or object-valued attributes, not occurring in this example) which are applied to objects or object collections. In the example, the following navigation expressions can be stated. The first line(s) shows the OCL expression and the last line the evaluation result and the type of the expression and the result.
bob.manuscript sub_17 : Paper
bob.manuscript.referee
Set{ada} : Set(Researcher)
cyd.manuscript.referee.manuscript.referee
Bag{ada} : Bag(Researcher)
sub_17.author->union(sub_17.referee)
Set{ada,bob} : Set(Researcher)
Collections: Collections can be employed in OCL to merge different elements into a single structure containing the elements. There are four collection kinds: sets, bags, sequences and ordered sets. Sets and ordered sets can contain an element at most once, whereas bags and sequences may contain an element more than once. In sets and bags the element order is insignificant, whereas sequences and ordered sets are sensitive to the element order. For a given class, the operation allInstances yields the set of current objects in the class.
Paper.allInstances
Set{sub_17,sub_18} : Set(Paper)
let P=Paper.allInstances in P.referee->union(P.author)
Bag{ada,bob,bob,cyd} : Bag(Researcher)
Paper.allInstances->sortedBy(p|p.wordCount)
Sequence{sub_18,sub_17} : Sequence(Paper)
Sequence{bob,ada,bob,cyd,ada}->asOrderedSet
OrderedSet{bob,ada,cyd} : OrderedSet(Researcher)
Collection operations: There is a number of collection operations which contribute essentially to the expressibility of OCL and which are applied with the ar- row operator. Among further operations, collections can be tested on emptiness (isEmpty, notEmpty), the number of elements can be determined (size), the elements can be filtered (select, reject), elements can be mapped to a different item (collect) or can be sorted(sortedBy), set-theoretic operations may be employed (union, intersection), and collections can be converted into other collection kinds (asSet, asBag, asSequence, asOrderdSet). Above, we have already used the collection operations union, sortedBy, and asOrderedSet.
Paper.allInstances->isEmpty false : Boolean
Researcher.allInstances->size 3 : Integer
Researcher.allInstances->select(r | not r.isStudent)
Set{ada,cyd} : Set(Researcher)
Paper.allInstances->reject(p | p.studentPaper)
Set{sub_17} : Set(Paper)
Paper.allInstances->collect(p | p.author.name)
Bag{’Bob’,’cyd’} : Bag(String)
Boolean-valued expressions: Because OCL is a constraint language, boolean expres- sions which formalize model properties play a central role. Apart from typical boolean connectives (and, or, not, =, implies, xor), universal and existen- tial quantification are available (forAll, exists).
Researcher.allInstances->forAll(r,s | r<>s implies r.name<>s.name) true : Boolean
Paper.allInstances->exists(p |p.studentPaper and p.wordCount>4242) false : Boolean
Boolean expressions are frequently used to describe class invariants and operation pre- and postconditions.
Previous benchmarks
The previous benchmark posed general questions that concerned the validation and verification of properties in UML and OCL models. The questions came hand in hand with precise models in which the questions were made concrete. Questions were given names in order to reference them. The following questions were stated:
ConsistentInvariants: Is the model consistent? Is there at least one object diagram satisfying the UML class model and the explicit OCL invariants?
Independence: Are the invariants independent? Is there an invariant which is a consequence of the conditions imposed by the UML class model and the other invariants? Consequences: Is it possible to show that a stated new property is a consequence of the given model?
LargeState: Is it possible to automatically build valid object diagrams in a parameterized way with a medium-sized number of objects, e.g. 10 to 30 objects and appro- priate links, where all attributes take meaningful values and all links are established in a meaningful way? These larger object diagrams are intended to explain the used model elements (like classes, attributes and associations) and the constraints upon them by non-trivial, meaningful examples to domain experts not necessarily familiar with formal modeling techniques.
InstantiateNonemptyClass: Can the model be instantiated with non-empty populations for all classes?
InstantiateNonemptyAssoc: Can the model be instantiated with non-empty populations for all classes and all associations?
InstantiateDisjointInheritance: Can all classes be populated in presence of UML
generalization constraints like disjoint or complete?
InstantiateMultipleInheritance: Can all classes be populated in presence of multiple inheritance?
ObjectRepresentsInteger: Given a representation of the integers in terms of a UML class model where an integer is captured as a connected component in an object diagram. Is it true that any connected component of a valid object diagram either corresponds to the term zero or to a term of the form succn (zero) with n > 0 or to a term of the form predn (zero)?
IntegerRepresentsObject: Is it true that any term of the form zero or of the form succn (zero) or of the form predn (zero) corresponds to a valid object diagram for the model?
The concrete four UML and OCL models models that were used to make the questions precise were: CivilStatus (CS) [see Fig. 3], WritesReviews (WR) [see Fig. 2], DisjointSubclasses (DS) [see Fig. 4], and ObjectsAsIntegers (OAI) [see Fig. 5]. All details can be found in [13].
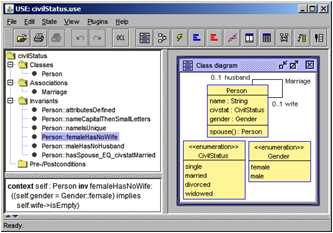
Fig. 3. Class Diagram for CS
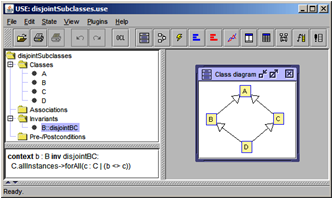
Fig. 4. Class Diagram for DS
Additional benchmarks
The two new benchmarks described in this section complement the old benchmarks with regard to the use of integer arithmetic and the construction of larger models for which aggregate functions (in the sense of SQL functions as count or min) are needed.
Integer arithmetic
As indicated in Fig. 6, for the integer arithmetic benchmark the respective class diagram only has one class with three integer attributes a, b, and c. Basically in this benchmark solutions for the equation a = b op c have to be found. The operator op is one of the basic OCL integer operators +, -, *, div. Exactly one of the four invariants from the lower left of Fig. 6 will be active.
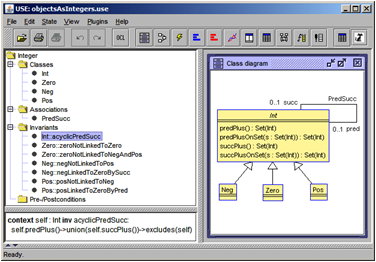
Fig. 5. Class Diagram for OAI
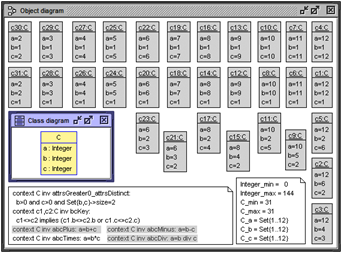
Fig. 6. Integer arithmetic benchmark
The benchmark asks for the construction of a number of C objects (in the example exactly 31) in which the respective operator invariant is valid. The other two invariants guarantee that the solutions in the found C objects are mutually distinct solutions, i.e., each solution appears only once.
We have used this benchmark to compare the efficiency of different SAT solvers that can be employed for the model validator available in the USE tool. The different SAT solvers (SAT4J, LightSAT4J, MiniSat, MiniSatProver) available under Windows show significantly different performance under this benchmark. Another instantiation of the benchmark for available SAT solvers under Linux confirmed the observations made for Windows.
Larger model with aggregation functions
The second new benchmark handles global invariants restricting many classes and concerns the construction of object diagrams for a State-Distict-Community world as shown in Fig. 7. States consist of districts that in turn consist of communities. Individual persons with four statistical attributes (female, young, degree, married) live in communities. The task is to construct an object diagram where in each geographical area (State, District, Community) the statistical distribution of the attributes follows the percentages (Pc) stated in the Config object.
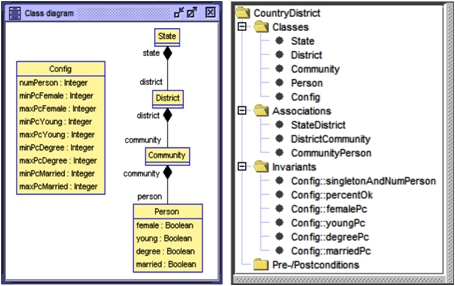
Fig. 7. Class diagram for State-District
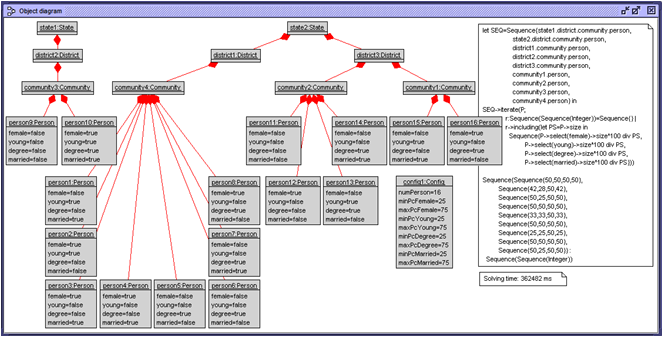
Fig. 8. Object diagram for Country-District
An example object diagram is presented in Fig. 8. For example, there the Config object requires that in each state, district and community the percentage of young people lies between 25% and 75% (minPcYoung and maxPcYoung). This example object diagram used 2 states, 3 districts, and 4 communities. The number of Person objects is also stated in the Config object.
The underlying invariants concern the three geographical areas and the four statistical attributes. The invariants also include a decent degree of integer arithmetic in order to restrict the statistical distribution of the attributes correctly. It took the USE model validator about 6 minutes to construct the example object diagram. This benchmark is well-suited for comparing the abilities of a UML and OCL analysis tool with regard to global constraints, integer arithmetic and the construction of middle-sized object diagrams.
Community Roadmap
Completing the benchmark is not something we can do on our own. And we shouldn’t either. The next subsections discuss three different community-driven actions to bring our proposal closer to reality.
Improving Benchmark Coverage
Our initial collection of benchmark models covers already a good number of interesting OCL expressions and scenarios but it is far from being complete. Speaking generally, for an OCL tool there are challenges in two dimensions: (a) challenges related to the expressiveness of OCL (i.e., the complete and accurate handling of OCL) and (b) challenges related to the computational complexity of the evaluating OCL for a given problem (verification, testing, code-generation,…).
Therefore, beyond increasing the number of benchmark models, we also require several variations of the same model, e.g. in terms of size and specific constructs used in the OCL constraints, to be part of the benchmark and improve this way it’s coverage. And each of these variations can be decomposed in a number of subvariations that are relevant too. For instance, wrt size variations, we can increase a model by adding more classes, more attributes per class, increasing its density (number of associations between classes), the number of constraints, or all of them at the same time. Some underlying formalisms are more sensitive than others to some of these variations so fair evaluations would require to play with all these extension variables.
This could easily lead to a combinatorial explosion. Still, based on our own expe- rience we believe that at least the following scenarios should be added to our current collection of benchmark models:
- Models with tractable constraints, i.e., constraints that can be solved ‘trivially’ by simple propagation steps.
- Models with hard, non-tractable constraints, e.g., representations of NP-hard problems.
- Unsatisfiable models, i.e. models that cannot be even instantiated in way that all constraints are satisfied.
- Highly symmetric problems, i.e., that require symmetry breaking to efficiently detect unsatisfiability
- Intensive use of Real arithmetic.
- Intensive use of String values and operations on strings. So far, String attributes are mostly ignored [5] or simply regarded as integers which prohibits the verification of OCL expressions including String operations other than equality and inequality.
- Many redundant constraints: is the approach able to detect the redundancies and benefit from them to speed up the evaluation?
- Sparse models: instances with comparably few links offer optimization opportunities that could be exploited by tools.
- Support for recursive operations, e.g. in form of fixpoint detection or static unfolding.
- Intensive use of the ‘full’ semantic of OCL (like the undefined value or collection semantics); this poses a challenge for the lifting to two-valued logics.
Recent research developments (e.g. [20]) could be enhanced to deal with OCL expressions and be employed to automatically generate some of these benchmark models, specially variations in size or density given a “seed” model. Nevertheless, making an effort to find and contribute industrial models is still key to make sure that tools face realistic models.
OCL repository
The easiest way to share and contribute models to a common benchmark is by storing them all in a single repository. This is not a new idea, several initiatives like MDEForge [18] or ReMODD [12] have been proposed before but with limited success, mainly due to their ambitious goal: a repository for all kinds of models (and other modeling artifacts) in any format, shape or size.
We aim for a less ambitious but more feasible goal, a repository for OCL-focused models. Being a textual language, the standard infrastructure for code hosting ser- vices/version control systems can be largely reused. We still need to store the models accompanying those OCL expressions but, in our scenario, they are basically only UML models and, mostly, limited to class diagrams which simplifies a lot their management.
Nowadays, the online coding platform GitHub (with over 30 million hosted projects) is the only reasonable choice to host such repository since it offers all the functionality we need and it is very well-known which reduces the entry barrier of possible contributors that are not forced to invest time learning a new environment. Therefore we have initialized our OCL repository there and added some basic instructions on how to contribute new UML/OCL models there.
OCL competitions
Competition is in our blood. Therefore, one way to increase awareness on the bench- mark is to organize yearly competitions of OCL tools where tool vendors evaluate their tools against each other by executing them on the same set of benchmark models.
This format is very successful in the SAT community (e.g. see 5 ) where winning a competition is considered a very prestigious achievement for a SAT solver and there- fore something that vendors/researchers strive for. In the MDE community we have the successful example of the Tool Transformation Contest6 , focusing on comparing the expressiveness, usability and performance of transformation tools to get a deeper understanding of their relative merits and identify open problems. We propose to replicate these successes in the OCL community
Typically, competitions are organized in different tracks depending on the properties we want to measure and, more importantly, include an initial call for problems / case studies to use in the competition itself. These proposals are perfect candidates to extend our benchmark.
Conclusions
This paper emphasizes the increasing need for a reliable set of OCL Benchmarks that can be used to consistently evaluate and compare OCL tools. We believe such bench- marks would encourage the development of new OCL tools (that now would have a way to evaluate their progress and contrast it against more established tools and a chance to distinguish themselves by focusing on those aspects where others may be failing) and increase the user base of OCL and other similar languages since users would be more confident on the tools’ capabilities.
This is still work in progress, and thus, we have also outlined how the community as a whole should (and could) push forward these ideas by, for instance, contributing to a common repository or organizing and participating in specific events on this topic. We hope to see these actions taking place in a near future.
References
- K. Anastasakis, B. Bordbar, G. Georg, and I. Ray. On Challenges of Model Transformation from UML to Alloy. Software and System Modeling, 9(1):69–86, 2010.
- B. Beckert, M. Giese, R. Hähnle, V. Klebanov, P. Rümmer, S. Schlager, and P. H. Schmitt. The KeY system 1.0 (Deduction Component). In F. Pfenning, editor, CADE, LNCS 4603, pages 379–384. Springer, 2007.
- A. Boronat and J. Meseguer. Algebraic Semantics of OCL-Constrained Metamodel Specifications. In M. Oriol and B. Meyer, editors, TOOLS (47), LNBIP 33, pages 96–115. Springer,2009.
- A. D. Brucker and B. Wolff. HOL-OCL: A Formal Proof Environment for UML/OCL. In L. Fiadeiro and P. Inverardi, editors, FASE, LNCS 4961, pages 97–100. Springer, 2008.
- F. Büttner and J. Cabot. Lightweight String Reasoning for OCL. In A. Vallecillo, J.-P.Tolvanen, E. Kindler, H. Störrle, and D. S. Kolovos, editors, ECMFA, LNCS 7349, pages 244–258. Springer, 2012.
- J. Cabot, R. Clarisó, and D. Riera. UMLtoCSP: A Tool for the Formal Verification of UM- L/OCL Models using Constraint Programming. In R. E. K. Stirewalt, A. Egyed, and B. Fis- cher, editors, ASE, pages 547–548. ACM, 2007.
- J. Cabot, J. Mazón, J. Pardillo, and J. Trujillo. Specifying aggregation functions in multidi- mensional models with OCL. In Proc. of the 29th Int. Conf. on Conceptual Modeling (ER 2010), pages 419–432, 2010.
- A. Calì, G. Gottlob, G. Orsi, and A. Pieris. Querying UML Class Diagrams. In L. Birkedal, editor, FoSSaCS, LNCS 7213, pages 1–25. Springer, 2012.
- K. C. Castillos, F. Dadeau, J. Julliand, and S. Taha. Measuring Test Properties Coverage for Evaluating UML/OCL Model-Based Tests. In B. Wolff and F. Zaïdi, editors, ICTSS, LNCS 7019, pages 32–47. Springer, 2011.
- J. D. Chimiak-Opoka and B. Demuth. A Feature Model for an IDE4OCL. ECEASST, 36,2010.
- M. Clavel, M. Egea, and M. A. G. de Dios. Checking Unsatisfiability for OCL Constraints.Electronic Communications of the EASST, 24:1–13, 2009.
- R. B. France, J. M. Bieman, S. P. Mandalaparty, B. H. C. Cheng, and A. C. Jensen. Repository for model driven development (remodd). In 34th Int. Conf. on Software Engineering, ICSE2012, pages 1471–1472, 2012.
- M. Gogolla, F. Büttner, and J. Cabot. Initiating a benchmark for UML and OCL analysis tools. In Proc. of 7th Int. Conf. on Tests and Proofs, pages 115–132, 2013.
- M. Gogolla, F. Büttner, and M. Richters. USE: A UML-Based Specification Environment for Validating UML and OCL. Science of Computer Programming, 69:27–34, 2007.
- C. A. Gonzalez, F. Büttner, R. Clariso, and J. Cabot. EMFtoCSP: A Tool for the Lightweight Verification of EMF Models. In S. Gnesi, S. Gruner, N. Plat, and B. Rumpe, editors, Proc. ICSE 2012 Workshop Formal Methods in Software Engineering: Rigorous and Agile Approaches (FormSERA), 2012.
- H. Hußmann, B. Demuth, and F. Finger. Modular Architecture for a Toolset Supporting OCL. Sci. Comput. Program., 44(1):51–69, 2002.
- A. Queralt, A. Artale, D. Calvanese, and E. Teniente. OCL-Lite: Finite Reasoning on UM- L/OCL Conceptual Schemas. Data Knowl. Eng., 73:1–22, 2012.
- J. D. Rocco, D. D. Ruscio, L. Iovino, and A. Pierantonio. Collaborative repositories in model-driven engineering. IEEE Software, 32(3):28–34, 2015.
- M. Roldán and F. Durán. Dynamic Validation of OCL Constraints with mOdCL. ECEASST,44, 2011.
- O. Semeráth, A. Vörös, and D. Varró. Iterative and incremental model generation by logic solvers. In Fundamental Approaches to Software Engineering – 19th International Confer- ence, FASE 2016, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2016, Eindhoven, The Netherlands, April 2-8, 2016, Proceedings, pages87–103, 2016.
- R. Wille, M. Soeken, and R. Drechsler. Debugging of Inconsistent UML/OCL Models. In
- W. Rosenstiel and Thiele, editors, DATE, pages 1078–1083. IEEE, 2012.
- E. D. Willink. Re-Engineering Eclipse MDT/OCL for Xtext. ECEASST, 36, 2010.
- K. Yatake and T. Aoki. SMT-Based Enumeration of Object Graphs from UML Class Dia- grams. ACM SIGSOFT Software Engineering Notes, 37(4):1–8, 2012.
FNR Pearl Chair. Head of the Software Engineering RDI Unit at LIST. Affiliate Professor at University of Luxembourg. More about me.



+1
For simple OCL, there will probably be agreement between intuitively correct and the specification wording.
For more interesting OCL, a new benchmark may contribute to discussion on what the specification should actually say.