In this discussion thread , a reader complains about the challenges of modeling complex queries in OCL due to its lack of advanced aggregate and analytical operations. Unfortunately, this is true. However, this library is missing some of the most typical operators (at least typical for those of you familiar with SQL) when it comes to write interesting queries: min, max, avg, rank, percentile,…
The good news is that it’s not that difficult to add these operations to the standard (or at least to your own models) by building on top of the existing ones. This is why I “recover” this paper (presented at the ER conference) where we show how to extend OCL with a predefined set of aggregation functions (including the ones mentioned above). Our extension facilitates the defiinition of platform-independent query operations as part of the specification of any software system. In particular, we show the benefits of these functions when defining the conceptual multidimensional model of a data warehouse.
You can also take a look at the presentation.
Or read the full paper (here or below)
Specifying Aggregation Functions in Multidimensional Models with OCL
1 Introduction
Data warehouse systems support decision makers in analyzing large amounts of data integrated from heterogeneous sources into a multidimensional model. Several authors [1–4] and benchmarks for decision support systems (e.g., TPC-H or TPC-DS [5]) have highlighted the great importance of aggregation functions during this analysis to compute and return a unique summarized value that represents all the set, such as sum, average or variance.
Although it is widely accepted that multidimensional structures should be represented in an implementation-independent conceptual model to reflect real-world situations as accurately as possible [6], multidimensional queries that satisfy information needs of decision makers are not currently expressed at the conceptual level but only after the rest of the data warehouse system has been developed. Therefore, the definition of these queries is implementation- dependent, which requires a lot of effort and expertise in the target implementation platform. The main drawback of this traditional way of proceeding is that it avoids designers to properly validate if the conceptual schema meets the requirements of decision makers before the final implementation. Therefore, if any change is found out after the implementation, designers must start the whole process from the early stages, thereby dramatically increasing the overall cost of data warehouse projects. As stated by Olivé [7], this main drawback comes from the little importance given to the informative function of the information system, that is, to the definition of queries at the conceptual level that must be provided to the users to satisfy their information needs. To overcome this drawback in the data warehouse scenario, multidimensional queries must be defined at the conceptual level.
The main restriction for defining multidimensional queries at the conceptual level is the rather limited support offered by current conceptual modeling languages [8–11], that exhibit a lack of rich constructs for the specification of aggregation functions. So far, researchers have focused on using a small subset of them, namely sum, max, min, avg and count [12] (and most modeling languages do not even cover all these basic ones). However, data warehouse systems require aggregation functions for a richer data analysis [6, 4]. Therefore, we believe that it is highly important to be able to provide a wide set of aggregation functions as predefined constructs offered by the modeling language used in the specification of the data warehouse so that the definition of multidimensional queries can be carried out at the conceptual level. This way, designers can define and validate them regardless the final technology platform chosen to implement the data warehouse.
To this aim, in this paper, the standard Object Constraint Language (OCL [13]) library is extended with a new set of aggregation functions to facilitate the specification of multidimensional queries as part of the definition of UML conceptual schemas. In our work, we will use the operations in combination with our UML profile for multidimensional modeling [14]. Nevertheless, our OCL extension is independent of the UML profile and could be used in the definition of any standard UML model. Our new OCL operations have been tested and implemented in the USE tool [15] in order to ensure their well-formedness and to validate them on sample data from our running example (see Sect. 2).
Our work is aligned with current Model-Driven Development (MDD) approaches, such those of [16, 17], where the implementation of the system is supposed to be (semi)automatically generated from its high-level models. The definition of all multidimensional queries at the conceptual level permits a more complete code-generation phase, including the automatic translation of these queries from their initial platform-independent definition to the final (platform-dependent) implementation, as we describe later in the paper. Therefore, code can be easily generated for implementing multidimensional queries in several languages, such as MDX or SQL.
The remainder of this paper is structured as follows: a motivating example is presented in the next section to illustrate the benefits of our proposal throughout the paper. Our OCL extension to model this kind of queries at the conceptual level is presented in Sect. 3, while its validation is carried out in Sect. 4. Sect. 5 defines how to automatically implement it. Finally, Sect. 6 comments the related work and Sect. 7 presents the main conclusions and sketches future work.
2 Motivating Example
To motivate the importance of our approach and illustrate its benefits, consider the following example, which is inspired in one of the scenarios described in [18]: an airline’s marketing department wants to analyze the flight activity of each member of its frequent flyer program. The department is interested in seeing what flights the company’s frequent flyers take, which planes they travel with, what fare basis they pay, how often they upgrade, and how they earn their frequent flyer miles…
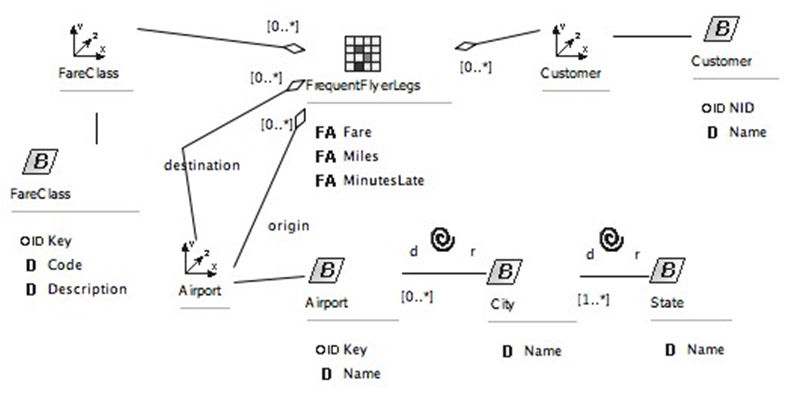
A possible conceptual model for this example is shown in Fig. 1 as a class diagram annotated and displayed using the multidimensional UML profile presented in [14]. The figure represents a multidimensional model of the flight legs taken by frequent flyers in the FrequentFlyerLegs Fact class. This class contains several FactAttribute properties: Fare, Miles and MinutesLate. These properties are measures that can be analyzed according to several aspects as the origin and destination airport (Dimension class Airport ), the Customer, FareClass, Flight and Date (these two last Dimension classes are not detailed in the diagram).
Fig. 1. Conceptual multidimensional model for our frequent flyer scenario.
Given this conceptual multidimensional model, decision makers can request a set of queries to retrieve useful information from the system. For instance, they are probably interested in knowing the miles earned by a frequent flyer in his/her trips from a given airport ( e.g., airports located in Denver) in a given fare class. Many other multidimensional queries can be similarly defined. This kind of queries are usually of particular interest for the decision makers because they (i) aggregate the data (e.g., the earned miles in the previous example) and (ii) summarize values by means of different aggregation functions. For example, it is likely that decision makers will be interested in knowing the total number of miles earned by the frequent flyer, a ranking of frequent flyers per number of miles earned, the average number of earned miles, several percentiles on the number of miles and so forth. Interestingly, these multidimensional queries are related to several concepts [19]:
- Phenomenon of interest, which is the measure or set of measures to analyze (FactAttribute properties in Fig. 1). Miles are the phenomenon of interest in the previous defined query.
- Category attributes, which are the context for analyzing the phenomenon of interest (Dimension and Base classes in Fig. 1). E.g., FareClass and Airport are category attributes.
- Aggregation sets, which are subsets of the phenomenon of interest according to several category attributes. In our sample query, the aggregation set only contains miles obtained by frequent flyers that depart from Denver.
- Aggregation functions, which are predefined operators that can be applied on the aggregation sets to summarize or analyze their factual data. E.g., the sum, avg or percentile operators above-mentioned.
The first two aspects (i.e., the definition of the category attributes and the phenomenon of interest) can be easily modeled in UML (as we have already accomplished in Fig. 1). Furthermore, a method for defining aggregation sets in OCL has been proposed in [16]. Regarding aggregation functions, so far, researchers and practitioners have focused on using a small subset of them, namely sum, max, min, avg and count [12]. Moreover, query-intensive applications, such as data warehouses or OLAP systems, require other kind of statistical functions for a richer data analysis (e.g., see [4]). However, support for statisti- cal functions is very limited (e.g., OCL does not even support all the basic aggregation functions) which hinders designers wanting to directly implement the kind of queries presented above and preventing them from easily satisfying the user requirements.
Therefore, we believe that it is highly important to be able to provide all kinds of aggregation functions as predefined constructs offered by the modeling language (UML and OCL in our case) so that the definition of multidimensional queries can be carried out at the conceptual level to define and val- idate them regardless the final technology platform chosen to implement the data warehouse. In the rest of the paper, we propose an extension for the OCL language to solve this issue.
3 Extending OCL with Aggregation Functions
Conceptual modeling languages based on visual formalisms are commonly managed together with textual formalisms, since some model elements are not easily or properly mapped into the graphical constructs provided by the modeling lan- guage [20]. For UML schemas, OCL [13] is typically used for this purpose. The goal of this section is to extend the OCL with a new set of predefined aggregation functions to facilitate the definition of multidimensional queries on UML schemas.
The set of core aggregation functions included in our study are those among the most used in data analysis [4]. To simplify their presentation, we classify these functions in three different groups, following [21, 3]:
- Distributive functions, which can be defined by structural recursion, i.e., the input collection can be partitioned into subcollections that can be individually aggregated and combined.
- Algebraic functions, which are expressed as finite algebraic expressions over distributive functions, e.g., average is computed using count and sum.
- Holistic functions, which are all other functions that are not distributive nor algebraic.
These functions can be combined to provide many other advanced operators. An example of such an operator is top(x) which uses the rank operation to return a subset of the x highest values within a collection.
3.1 Preliminary OCL Concepts
OCL is a rich language that offers predefined mechanisms for retrieving the values of the attributes of an object, for navigating through a set of related objects, for iterating through a collection of objects (e.g., by means of the forAll, exist and select iterators) and so forth. As part of the language, a standard library including a predefined set of types and a list of predefined operations that can be applied on those types is also provided. The types can be primitive (Integer, Real, Boolean and String ) or collection types (Set, Bag, OrderedSet and Sequence ). Some examples of operations provided for those types are: and, or, not (Boolean), +, −, ∗, >, < (Real and Integer), union, size, includes, count and sum (Set).
All these constructs can be used in the definition of OCL constraints, derivation rules, queries and pre/post-conditions. In particular, definition of queries follows the template:
context Class::Q(p1:T1, . . . , pn:Tn): Tresult
body: Query-ocl-expression
where the query Q returns the result of evaluating the Query−ocl−expression by using the arguments passed as parameters in its invocation on an object of the context type C lass. Apart from the parameters p1 . . . pn, in query-ocl-expression designers may use the implicit parameter self (of type C lass) representing the object on which the operation has been invoked.
As an example, the previous query total miles earned by a frequent flyer in his/her trips from Denver in a given fare can be defined as follows:
context Customer::sumMiles(FareClass fc)
body: self.frequentFlyerLegs−>select(f | f.fareClass=fc and f.origin.city.name=’Denver’)−>sum()
Unfortunately, many other interesting queries cannot be similarly defined since the operators required to define such queries are not part of the standard library (e.g. the average number of miles earned by a customer in each flight leg, since the average operation is not defined in OCL). In the next section, we present our extension to the OCL standard library to include them as predefined operators available to all users of this language.
3.2 Extending the OCL Standard Library
Multidimensional queries cannot be easily defined in OCL since the aggregation functions required to specify them are not part of the standard library and thus, they must be manually defined by the designer every time they are needed which is an error-prone and time-consuming activity (due to the complexity of some aggregation functions).
To solve this problem, we propose in this section an extension to the OCL Standard Library by predefining a list of new aggregation functions that can be reused by designers in the definition of their OCL expressions.
The new operations are formally defined in OCL by specifying their operation contract, exactly in the same style that existing operations in the library are defined in the OCL official specification document. Our extension does not change the OCL metamodel and thus, it does not risk the standard level of UML/OCL models using it. In fact, our operations could be regarded as new user-defined operations, a possibility which is supported by most current OCL tools. Therefore, our extension could be easily integrated in those tools.
Each operation is attached to the most appropriate (primitive or collection) type. As usual, functions defined on a supertype can be applied on instances of the subtypes. For each operation we indicate the context type, the signature and the postcondition that defines the result computed by it. When required, preconditions restricting the operation application are also provided. Note that some aggregation functions may have several slightly different alternative definitions in the literature. Due to space limitations, we stick to just one of them.
These functions can be called within OCL expressions in the same way as any other standard OCL operation. See an example in Sect. 3.3.
Distributive Functions
– MAX: Returns the element in a non-empty collection of objects of type T with the highest value. T must support the >= operation. If several elements share the highest value, one of them is randomly selected.
context Collection::max():T
pre: self−>notEmpty()
post: result = self−>any(e | self−>forAll(e2 | e >= e2))
– MIN: Returns the element with the lowest value in the collection of objects of type T . T must support the <= operation. If several elements share the lowest value, one of them is randomly selected.
context Collection::min():T
pre: self−>notEmpty()
post: result = self−>any(e | self−>forAll(e2 | e <= e2))
– SUM: Returns the sum value of the elements in the collection. Already part of the OCL Standard Library, and thus, we do not need to redefine it.
– COUNT: Returns the number of elements in a collection. Equivalent to the existing OCL size operation.
– COUNT DISTINCT: Returns the number of different elements in a col- lection. To implement this operation we convert the collection to a set (to remove repeated elements) and apply the OCL size operation to the resulting set.
context Collection::countDistinct(): Integer
post: result = self−>asSet()−>size()
Algebraic Functions
– AVG: Returns the arithmetic average value of the elements in the non-empty collection. The type of the elements in the collection must support the + and / operations.
context Collection::avg():Real
pre: self−>notEmpty()
post: result = self−>sum() / self−>size()
– VARIANCE: Returns the variance of the elements in the collection. The type of the elements in the collection must support the +, −, ∗ and / operations. The function accumulates the deviation of each element regarding the average collection value (this is computed by using the iterate operator: for each element e in the collection, the acc variable is incremented with the square result of substracting the average value from e). Note that this function uses the previously defined avg function.
context Collection::variance():Real
pre: self−>notEmpty()
post: result = (1/(self−>size()-1)) * self−>iterate(e; acc:Real =0 | acc + (e – self−>avg()) * (e – self−>avg()))
– STDDEV: Returns the standard deviation of the elements in the collection.
context Collection::stddev():Real
pre: self−>notEmpty()
post: result = self−>variance().sqrt()
– COVARIANCE: Returns the covariance value between two ordered sets (or sequences). We present the version for OrderedSets. The version for the Sequence type is the same, only the context type changes. The standard at operation returns the position of an element in the ordered set. As guaranteed by the operation precondition, both input collections must have the same number of elements.
context OrderedSet::covariance(Y: OrderedSet):Real pre: self−>size() = Y−>size() and self−>notEmpty() post: let avgY:Real = Y−>avg() in
let avgSelf:Real = self−>avg() in result = (1/self−>size()) * self−>iterate(e; acc:Real=0 | acc +
((e – avgSelf ) * (Y−>at(self−>indexOf(e)) – avgY))
Holistic Functions
– MODE: Returns the most frequent value in a collection.
context Collection::mode(): T
pre: self−>notEmpty()
post: result = self−>any(e | self−>forAll(e2 | self−>count(e) >= self−>count(e2))
– DESCENDING RANK: Returns the position (i.e., ranking) of an element within a Collection. We assume that the order is given by the >= relation among the elements (the type T of the elements in the collection must support this operator). The input element must be part of the collection. Repeated values are assigned the same rank value. Subsequent elements have a rank increased by the number of elements in the upper level. As mentioned above, this is just one of the possible existing interpretations for the rank function. Others would be similarly defined.
context Collection::rankDescending(e: T): Integer
pre: self−>includes(e)
post: result = self−>size() – self−>select(e2 | e >= e2)−>size() + 1
– ASCENDING RANK: Inverse of the previous one. The order is now given by the <= relation.
context Collection::rankAscending(e: T): Integer
pre: self−>includes(e)
post: result = self−>size() – self−>select(e2 | e <= e2)−>size() + 1
– PERCENTILE: Returns the value of the percentile p, i.e., the value below which a certain percent p of elements fall.
context Collection::percentile(p: Integer): T
pre: p >= 0 and p <= 100 and self−>notEmpty()
post: let n: Real = (self−>size()-1) * 25 / 100 + 1 in
let k : Integer = n.floor() in let d : Real = n – k in
let s: Sequence(Integer) = self−>sortedBy(e | e) in
if k = 0 then s−>first() * 1.0
else if k = s−>size() then s−>last() * 1.0
else s−>at(k) + d * (s−>at(k+1) – s−>at(k) ) endif
endif
– MEDIAN: Returns the value separating the higher half of a collection from the lower half, i.e., the value of the percentile 50.
context Collection::median(): T
pre: self−>notEmpty()
post: result = self−>percentile(50)
3.3 Applying the Operations
As we above-commented, these operations can be used exactly in the same way as any other standard OCL function. As an example, we show the use of our avg function to compute the average number of miles earned by a customer in each flight leg.
context Customer::avgMilesPerFlightLeg():Real
body: self−>frequentFlyerLegs.Miles−>avg()
4 Validation
Our OCL extension has been validated by using the UML Specification Environment (USE) tool [15]. As a first step, we have implemented our aggregation operations as new user-defined functions in USE. Thanks to the syntactic analysis performed by USE, the syntactic correctness of our functions has been proved in this step. Additionally, in order to also prove that our functions behave as ex- pected (i.e. to check that they are also semantically correct), we have evaluated them over sample scenarios and evaluated the correctness of the results (i.e., we have compared the result returned by USE when executing queries including our operations with the expected result as computed by ourselves).
Fig. 2 shows more details of the process. In the background of the USE environment we can see the implementation of the multidimensional conceptual schema of Fig. 1 in USE (left-hand side) and the script that loads the data provided in [18] (objects and links, which have been obtained by using the operations described in [16]) into the corresponding classes and associations (right-hand side). In the foreground we show one of the queries we have used to test our functions (in this case the query is used to check our avg function) together with the resulting collection of data returned by the query. It is worth noting that during the validation process, we have overcome some limitations of the USE tool, since it neither provides the indexOf nor Cartesian product functions. Therefore, functions that make use of these OCL operators needed to be slightly redefined for their implementation in USE, e.g., the covariance function.
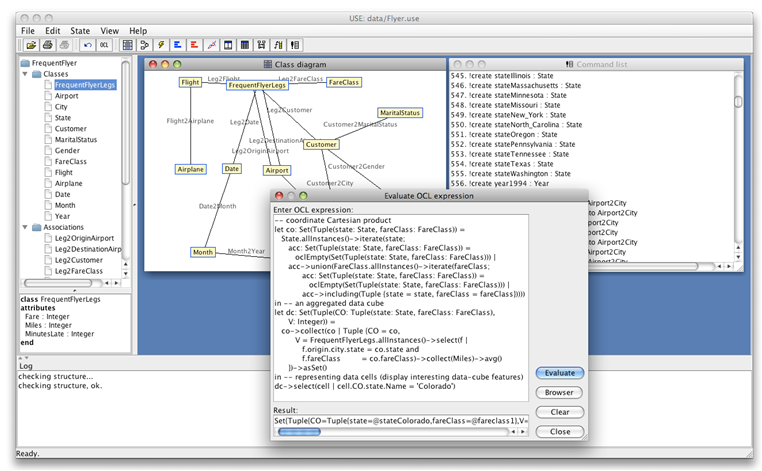
Fig. 2. Conceptual querying of frequent flyer legs implemented in USE
5 Automatic Code Generation
This section shows how our “enriched” schema can be used in the context of a MDD process. In fact, conceptual schemas containing queries defined using our aggregation functions can be directly implemented in any final technology platform by using exactly the same existing MDD methods and tools able to generate code from UML/OCL schemas. These methods do not need to be extended to cope with our aggregation functions. An automatic code-generation is possible thanks to the fact that (i) our library is defined at the model-level and thus it is technologically- independent, and (ii) aggregation functions are specified in terms of standard OCL operations.
More specifically, given a query operation q including an OCL aggregation operation s, q can be directly implemented in a technology platform p (for instance a relational database or a object-oriented Java program) if p offers a native support for s. In that case, we just need to replace the call to s with the call to the corresponding operation in p as part of the usual translation process followed to generate the code for implementing OCL queries in that platform. Otherwise, i.e., p does not support s, we need to first unfold s in q by replacing the call to s with the body condition of s. After the unfolding, q only contains standard OCL functions and therefore can be implemented in p as explained in the former case.
As an example, we show in Fig. 3 the implementation of the query average miles per flight leg specified in OCL in Sect. 3.3. Fig.3 (a) shows the implementation for a relational database, while Fig.3 (b) shows it for a Java program.
In the database implementation, queries could be translated as views. The generation of the relational tables (for the classes and associations in the conceptual schema) and the views for the query operations can be generated with the DresdenOCL tool [22] (among others). Since database management systems usu-ally offer statistical packages for all of our functions, the avg operation in the query is directly translated by calling the predefined SQL AVG function in the database (see Fig.3 (a)). For the Java example, queries are translated as methods in the class owning the query. Java classes and methods can be generated from a UML/OCL specification using the same DresdenOCL tool or other OCL-to-Java tools (see a list in [23]. However, in this case we need to first unfold the definition of avg in the query since Java does not directly support aggregation operations. The new OCL query body becomes:
context Customer::avgMilesPerFlightLeg():Real
post: result = self−>frequentFlyerLegs.Miles−>sum() / self−>frequentFlyerLegs.Miles−>size()
This new body is the one passed over to the Java code-generation tool to obtain the corresponding Java method, as can be seen in Fig. 3 (b). All non-standard Java operations (e.g., sumMiles ) are implemented by the own OCL- to-Java tool during the translation (basically they traverse the AST of the OCL expression and generate a new auxiliary method for each node in the tree without a exact mapping to one of the predefined methods in the Java API). Obviously, different tools will generate different Java code excerpts.
create view AvgMilesFlight as {
select avg(l.miles)
from customer c, frequentflyerlegs l
where c.id=l.customer
}
(a) DBMS code
class Customer {
int id; String name; Vector<FrequentFlyerLegs> f;
…
public float avgMiles() {
return sumMiles(f)/f.size();
} }
(b) Java code
Fig. 3. Code excerpts for an OCL query using the avg function
6 Related Work
Multidimensional modeling languages (and modeling languages in general) offer a limited support for the definition of aggregation operations at the conceptual level. Early approaches [9, 10, 24] are only concerned about static aspects and lack of mechanisms to properly model multidimensional query behavior. At most, these approaches suggest a limited set of predefined aggregation functions but without providing a formal definition. Recently, other approaches have been trying to use more expressive constructs to model aggregation functions at the conceptual level by extending the UML [8, 14, 11]. They all propose to use OCL to complete the multidimensional model with information about the applicable aggregation functions to define multidimensional queries properly. They also suggest that aggregation functions should be defined in the UML schema, but unfortunately, they do not provide any mechanisms to carry it out. Therefore, to overcome this drawback, we define in this paper how to extend OCL with new aggregation functions to query multidimensional schemas at the conceptual level. A subset of these functions was presented in a preliminary short paper [25].
7 Conclusions and Future Work
Aggregation functions should be part of the predefined constructs provided by existing languages for multidimensional modeling to allow designers to specify queries at the conceptual level. However, due to the current lack of support in modeling languages, queries are not currently defined as part of the conceptual schema but added only after the schema has been implemented in the final platform. In this paper, we address this issue by providing an OCL extension that predefines a set of aggregation functions that facilitate the definition of platform-independent queries as part of the specification of the multidimensional conceptual schema of the data warehouse. These queries can be then animated and validated at design-time and automatically implemented along with the rest of the system during the code-generation phase.
Our short term future work is to better integrate these aggregation functions with OLAP operations already presented in [16] to provide a more complete definition of the CS Furthermore, definition of multidimensional queries at the conceptual level opens the door to the development of systematic techniques for the treatment of aggregation problems in data analysis at the conceptual level, as a way to evaluate the overall quality of the data warehouse at design time. Finally, we are also concerned about developing mechanisms that help users to define their own ad-hoc ocl queries in a more intuitive manner.
References
- Cabibbo, L., Torlone, R.: A framework for the investigation of aggregate functions in database queries. In: ICDT. (1999) 383–397
- Lenz, H.J., Thalheim, B.: OLAP databases and aggregation functions. In: SSDBM, IEEE Computer Society (2001) 91–100
- Lenz, H.J., Thalheim, B.: OLAP schemata for correct applications. In: TEAA. (2005) 99–113
- Ross, R.B., Subrahmanian, V.S., Grant, J.: Aggregate operators in probabilistic databases. J. ACM 52(1) (2005) 54–101
- TPC: Transaction Processing Performance Council http://www.tpc.org.
- Rizzi, S., Abello, A., Lechtenborger, J., Trujillo, J.: Research in data warehouse modeling and design: dead or alive? In: DOLAP. (2006) 3–10
- Olivé, A.: Conceptual schema-centric development: A grand challenge for information systems research. In: CAiSE. (2005) 1–15
- Abello, A., Samos, J., Saltor, F.: YAM2: a multidimensional conceptual model extending UML. Inf. Syst. 31(6) (2006) 541–567
- Golfarelli, M., Maio, D., Rizzi, S.: The dimensional fact model: A conceptual model for data warehouses. Int. J. Cooperative Inf. Syst. 7(2-3) (1998) 215–247
- Hu¨semann, B., Lechtenb¨orger, J., Vossen, G.: Conceptual data warehouse model-ing. In: DMDW. (2000) 6
- Prat, N., Akoka, J., Comyn-Wattiau, I.: A UML-based data warehouse design method. Decision Support Systems 42(3) (2006) 1449–1473
- Shoshani, A.: OLAP and statistical databases: Similarities and differences. In: PODS, ACM Press (1997) 185–196
- Object Management Group: UML 2.0 OCL Specification. (2003)
- Luj´an-Mora, S., Trujillo, J., Song, I.Y.: A UML profile for multidimensional mod- eling in data warehouses. Data Knowl. Eng. 59(3) (2006) 725–769
- Gogolla, M., Bu¨ttner, F., Richters, M.: USE: A UML-based specification environment for validating UML and OCL. Sci. Comput. Program. 69(1-3) (2007) 27–34
- Pardillo, J., Mazon, J.N., Trujillo, J.: Extending OCL for OLAP querying on conceptual multidimensional models of data warehouses. Information Sciences 180(5) (2010) 584–601
- Mazon, J.N., Trujillo, J.: An MDA approach for the development of data ware- houses. Decis. Support Syst. 45(1) (2008) 41–58
- Kimball, R., Ross, M.: The Data Warehouse Toolkit. Wiley & Sons (2002)
- Rafanelli, M., Bezenchek, A., Tininini, L.: The aggregate data problem: A system for their definition and management. SIGMOD Record 25(4) (1996) 8–13
- Embley, D., Barry, D., Woodfield, S.: Object-Oriented Systems Analysis. A Model-Driven Approach. Youdon Press Computing Series (1992)
- Gray, J., Chaudhuri, S., Bosworth, A., Layman, A., Reichart, D., Venkatrao, M., Pellow, F., Pirahesh, H.: Data cube: A relational aggregation operator generalizing group-by, cross-tab, and sub totals. Data Min. Knowl. Discov. 1(1) (1997) 29–53
- Software Technology Group – Technische Universitat Dresden: Dresden OCL toolkit http://dresden-ocl.sourceforge.net/.
- Cabot, J., Teniente, E.: Constraint support in mda tools: A survey. In Rensink, A., Warmer, J., eds.: ECMDA-FA. Volume 4066 of Lecture Notes in Computer Science., Springer (2006) 256–267
- Sapia, C., Blaschka, M., Hofling, G., Dinter, B.: Extending the E/R Model for the Multidimensional Paradigm. In: ER Workshops. (1998) 105–116
- Cabot, J., Mazon, J.N., Pardillo, J., Trujillo, J.: Towards the conceptual specifi- cation of statistical functions with OCL. In: CAiSE Forum. (2009) 7–12
FNR Pearl Chair. Head of the Software Engineering RDI Unit at LIST. Affiliate Professor at University of Luxembourg. More about me.



As Jordi comments, and I would like to highlight: this work addresses the extension of OCL with aggregation functions in the context of a data warehouse, but it can be used for specifying aggregation functions in other kinds of software systems.