The modeling book
Site Sponsor
On verifying ATL transformations using ‘off-the-shelf’ SMT solvers
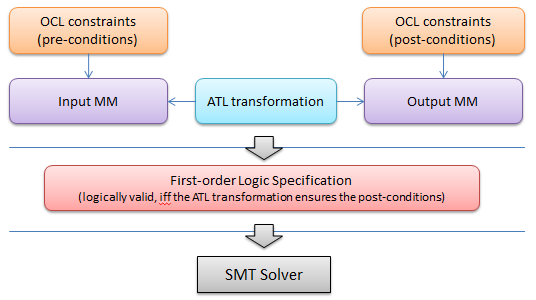
(post by Fabian Büttner) Recently, at this year’s MODELS conference, we (Fabian, myself and Marina Egea) have presented first results on the verification of ATL transformations using SMT solvers. In a nutshell, our approach allows us to verify that a declarative ATL transformation establishes all intended structural properties (i.e., transformation post-conditions, specified as OCL invariants) for the output metamodel. In short, we want to make sure the transformation always produce valid output models when applied on valid input models.
Technically, our approach consists of two steps:
- We first automatically derive a first-order logic (FOL) specification from the ATL transformation and the OCL constraints that we want to consider on the input and output metamodels. That is, we generate a signature of predicates and functions and a set of logical assertions over them.
- Then we use an SMT solver (we prefer Microsoft Z3) to check the properties. For each post-condition, we check whether the construction of a counter example is unfeasible.
In general, we generate a FOL specification that can represent models of arbitrary size. This means that we can conduct unbounded proofs for transformation correctness. As OCL, being part of the transformation, is known to be generally undecidable, the ATL verification problem is generally undecidable, too. However, for the case studies we have conducted so far (database schema transformations, state machine transformations), the Z3 solver could automatically prove all valid transformation properties fully automatically in less than a minute.
If you are interested in this line of research, please check out our MODELS paper or the slides of our presentation (below). All SMT files for Z3 (and, alternatively, for the Yices solver) are available online.
If you liked this post, you should subscribe to the blog feed or facebook page and follow my thoughts on twitter about software development or web design and social media .
[...] ATLTest – White box testing of (ATL) model transformations October 18, 2012 jordi No comments Recently, at MODELS 2012, we (Jordi and myself, Carlos González) had the opportunity to present our work titled “ATLTest: A White-Box Test Generation Approach for ATL Model Transformations”. As the title suggests, it’s a technique to generate input test models out of the analysis of the internals (white-box approach) of an ATL transformation. The idea is that these models can be later on used when testing the model transformation to get more accurate results about the “quality” of the transformation. Given the importance of model transformations (used in many different applications in MDE), some assurance about their correctness is needed. This testing approach complements our other formal verification approaches. [...]