Category theory meets model transformations

Category theory formalizes mathematical structures and its concepts in terms of a collection of objects and of arrows (also called morphisms). A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object.

To us (Zinovy Diskin, as the main intellectual perpetrator, Abel Gómez and myself), this seemed a natural way to represent the traceability links between model elements during a model transformation so we decided to explore what benefits category theory could bring to the world of model transformations if we formalized the notion of transformations, and in particular, the traceability mappings as abstract mathematical operations.

The results of our work have crystallized in the paper “Traceability Mappings as a Fundamental Instrument in Model Transformations” to be presented at the FASE’17 conference (20th International Conference on Fundamental Approaches to Software Engineering ).

Abstract:

Technological importance of traceability mappings for model transformations is well-known, but they have often been considered as an auxiliary element generated during the transformation execution and providing accessory information. This paper argues that traceability mappings should instead be regarded as a core aspect of the transformation de nition, and a key instrument in the transformation management.

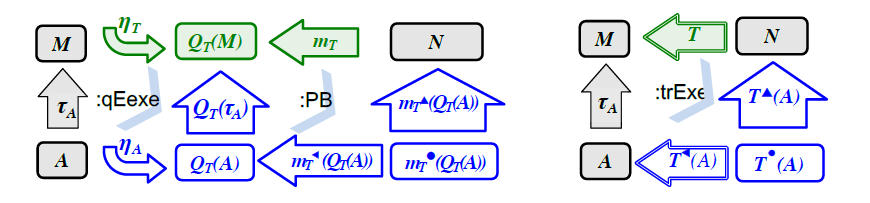
We will show how a transformation can be represented as the result of execution of a metamodel mapping, which acts as a special encoding of the transformation definition. Since mappings enjoy Boolean operations (as sets of links) and sequential composition (as sets of directed links), encoding transformations by mappings makes it possible to define these operations for transformations as well, which can be useful for model transformation reuse, compositional design, and chaining.

Read the complete article here